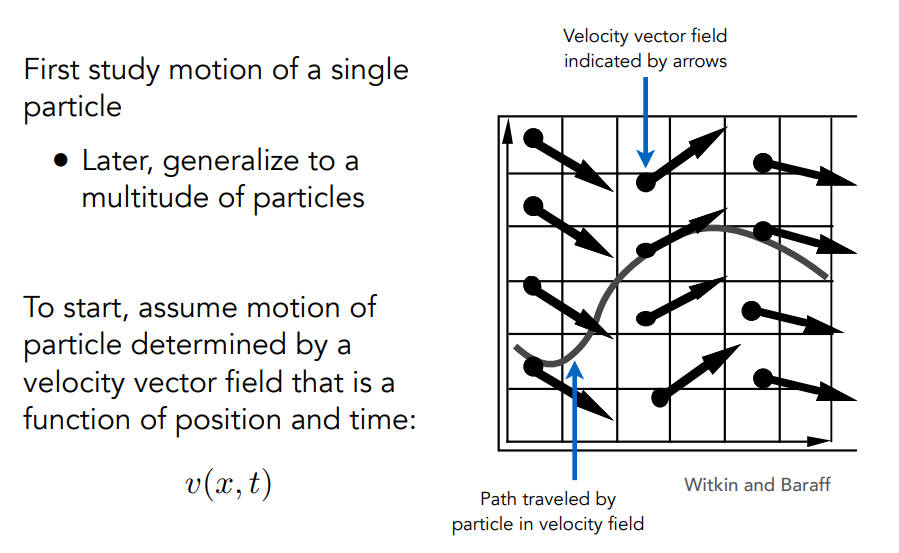
Single particle simulation
模拟一个粒子在速度场中如何运动
速度场:任何一个位置,都知道该粒子的速度
Ordinary Differential Equation (ODE)
常微分方程
常的意思就是只有一个变量(x,t不算),对x的微分,单变量的微分方程
Euler method
使用上一个时刻的量(速度,加速度)来计算当前时刻的量(位置、速度)
这个叫Explicit Euler或者Forward Euler
问题是不稳定
步长太长就会不准确,步长越小越精确
在一些特殊情况下,不管取多小的步长,都会偏移出去,比如螺旋形的速度场;头发型的速度场也会导致奇怪的结果,这种情况叫做正反馈,如果出现问题就会慢慢地无限放大
不稳定≠误差,因为无论多小的步长最后都会出问题
用数值的方法解微分方程会遇到的问题:
误差
不稳定 diverge(偏离)
Combating Instability
中点法(Midpoint Method)
选取一个步长t计算出位置a
计算两点中点b
然后按中点b的速度和之前的步长t来计算位置,得到c
为什么中点法更准确一点,是因为计算中多了一个二次的项
自适应步长(Adaptive Step Size)
就是自适应减小步长,将一个步长一分为二,做两次欧拉,而是否要一分为二,取决于$X_T和X_{\frac{T}{2}}$位置距离的远不远
最终的结果就是,在不同的位置会选用不同的步长来计算
隐式方法(Implicit Euler method也叫backward method)
- 当前一步使用下一个时间的derivatives(导数、梯度)
- 式子不好解
- 认为,当前位置和下一帧的加速度已知,两个式子解下一帧位置和下一帧速度
- $ x^ {t+\Delta t} $ = $ x^ {t} $ + $ \Delta $ $ t\dot x^ {t+\Delta t} $
- $\dot x^ {t+\Delta t} $ = $ \dot x^ {t} $ + $ \Delta $ $ t\ddot x^ {t+\Delta t} $
如何定义/量化
局部的误差/累计误差
阶,也就是误差和步长$\Delta t$之间的关系
隐式欧拉方法是一阶的:局部误差是$O(h^2)$,全局误差是$O(h)$,h就是步长
$O(h)$就是如果我把步长缩小到一半,那误差也缩小的一半
非基于物理的方法(Position - Based / Verlet Integration)
- 认为某一节弹簧,当被拉开后,会立刻回到原状,可以认为是一个劲度系数很大的弹簧,通过非物理的简化方式直接改变位置
Runge-Kutta Families
这是一类方法,很擅长解ODEs
这是4阶的方法,这个方法简称RK4
y就是一个位置,h是步长,每个k就是速度场中不同位置和时间的值,类似一个空间中的中点法
Rigid body simulation
刚体,不会发生形变,也就是会让内部所有的点按照同一种方式去运动
会考虑更多的物理量
- 角度、角速度、角加速度
Fluid simulation
A Simple Position-Based Method
key idea:
假设水是由刚体小球组成的
假设水都是不可压缩的,也就是水密度始终一致
直到水的分布就知道水的密度,当水的密度改变时,就需要将密度修正回来
就通过移动小球的位置来修正
我们需要知道任何一个点的密度对小球的位置的梯度,可以理解为,在一个点,小球的位置的改变会对密度产生改变,梯度就是衡量这个改变
然后就使用梯度下降法(gradient descent)
会产生停不下来的问题,所以在实际中人们会加入能量损失等方法来让模拟停止
Eulerian vs. Lagrangian
两种模拟一大堆物体的方法
上述模拟水的方法称为拉格朗日方法(Lagrangian),俗称质点法,会盯着物体的变化
解常微分方程称为欧拉方法,也叫网格法,会盯着一个网格的变化
Material Point Method (MPM)
混合方法,两种方法都考虑在内
Lagrangian:认为每个粒子都有着一种材质属性
Eulerian:在格子中做融化过程
Interaction:最后把格子的信息写回粒子上