Material == BRDF
- 材质就是:一个表面怎么被反射的
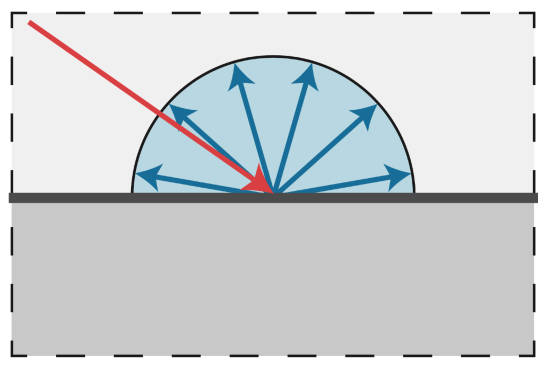
Diffuse/Lambertian Material
满足能量守恒,假设一个着色点均匀地吸收多少能量就均匀地发出多少能量即radiance==irradiance
然后经过推导,算出BRDF也就是f_r是$1/\pi$,这就是不吸收任何能量的BRDF
我们设定一个变量$\rho$为albedo反射率,范围是[0,1]
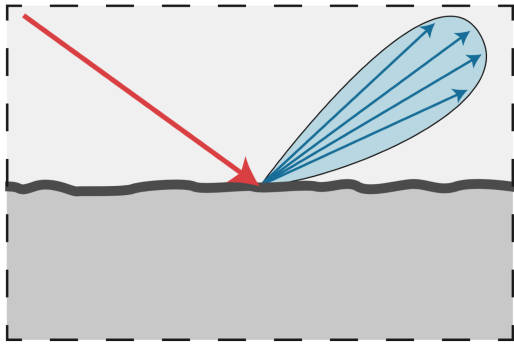
Glossy Material
- 金属类的材质,不会均匀反射而是往一个大致方向反射
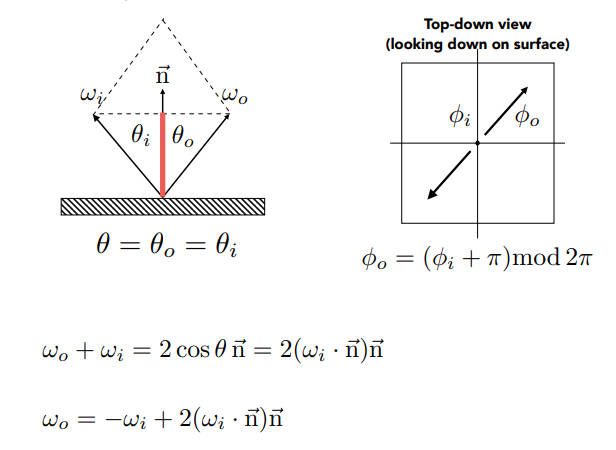
Perfect Specular Reflection
完美反射
方位角差$\pi$
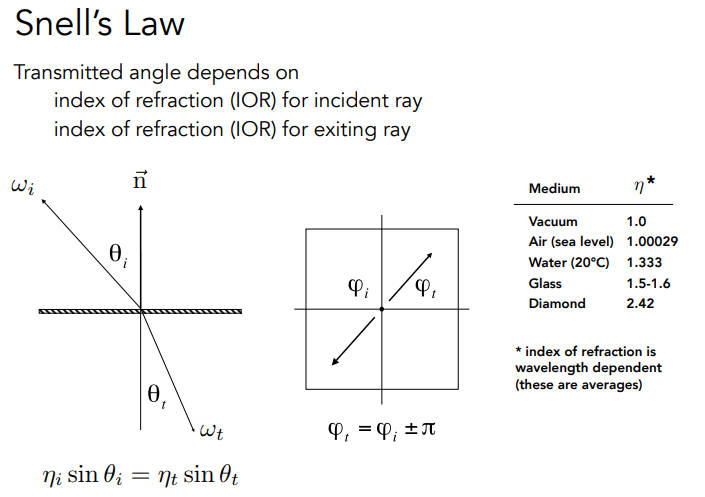
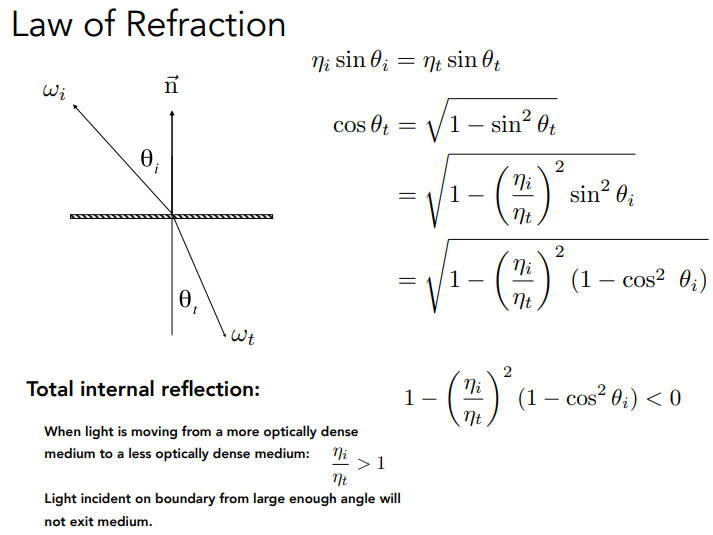
Specular Refraction - Snell’s Law
折射定律
根据折射率可以算出折射角
方位角差$\pi$
当入射的介质折射率大于折射的介质折射率就可能会出现没有折射,那么就是全反射
- 反射(BRDF)和折射(BTDF)可以统称BSDF,S代表的是散射
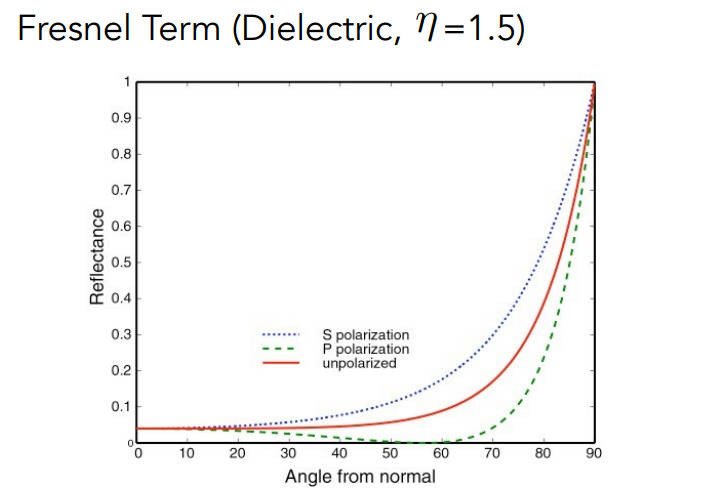
Fresnel Reflection/Term(菲涅尔项)
入射光和物体表面法线的夹角越大,越多的光被反射,夹角越小,越多的光被折射而很少被反射
- 比如一个实际的例子,在车里,后排乘客看前车玻璃看到的是车内司机,看后车玻璃看到的是车外景
极化现象,但一般光是由s极化和p极化组成的(也叫s偏振和p偏振)
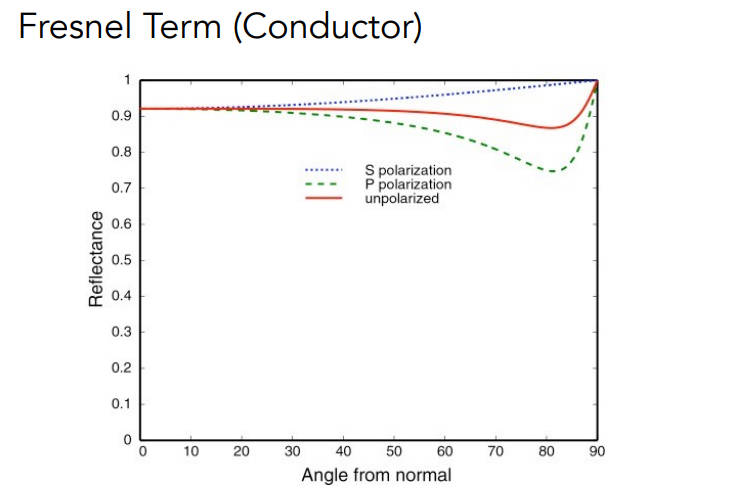
但对于导体而言,菲涅尔项不管角度如何都是很高的,也就是反射的光很多,这也是为什么会古代用铜和银做镜子
- 菲涅尔项公式,n1入射介质系数(折射率),n2折射介质系数,但公式太复杂,所以有了下面的简化公式
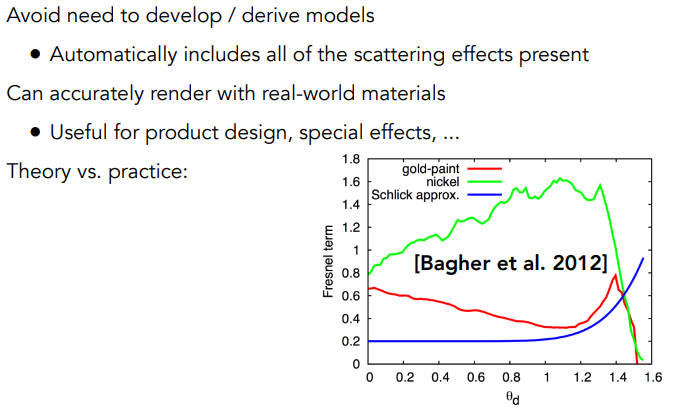
Schlick’s approximation:主旨就是拟合一条曲线,从一个值到1,绝缘体就从很小的数比如0开始,导体就从比较大的数开始,比如0.9,正常情况下,是个不错的近似
- 导体的折射率是负数,所以还要一个k系数
Microfacet Material(PBR)
当我们距离很远看一个物体表面时,很多微小的东西就看不到,最终能看到的是,表面对光的一个总体作用
每一个微表面理解成一个微小的镜面
也就是说,微表面模型,从远处看是材质外观,从近处看是几何
Microfacet BRDF
对于glossy材质,比较平,法线基本都朝上,所以法线会宏观得聚集在向上的一个小范围
对于diffuse材质,法线在方向上散的就比较开,所以分布范围就很广
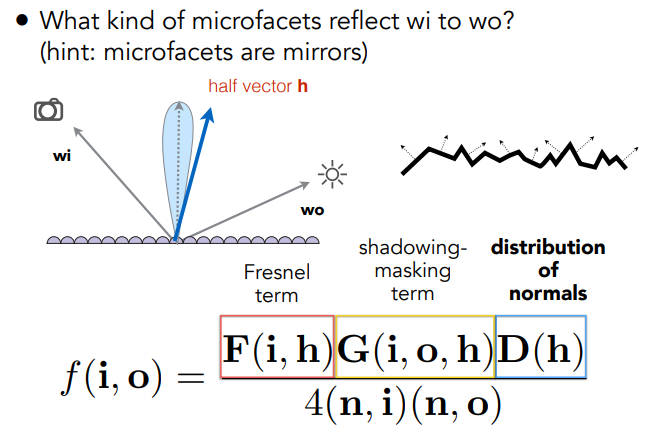
BRDF:
F(Fresnel term):首先考虑一个菲涅尔项(也就是说能反射多少光出来)
D(distribution of normals):法线分布,就是解决,有多少微表面能把光从wi反射到wo,因为只有微表面的法线方向和半程向量一致时,才会反射(把微表面当成镜子),所以就是D(h),在h方向上法线分布的一个查询
G(shadowing-masking term):自阴影,有一些微表面被另一些微表面挡住了,而失去了它们反射光的作用,在入射光几乎是平着打在平面上时,最容易发生这个现象,我们称这个角度为grazing angle
微表面模型问题:diffuse项很少,有时人们要认为添加一些漫反射
有很多微表面模型
Isotropic(各向同性)/Anisotropic(各向异性) Materials(BRDFs)
各向同性:微表面并不存在一定的方向性,或者方向性很弱
各向异性:微表面有方向性
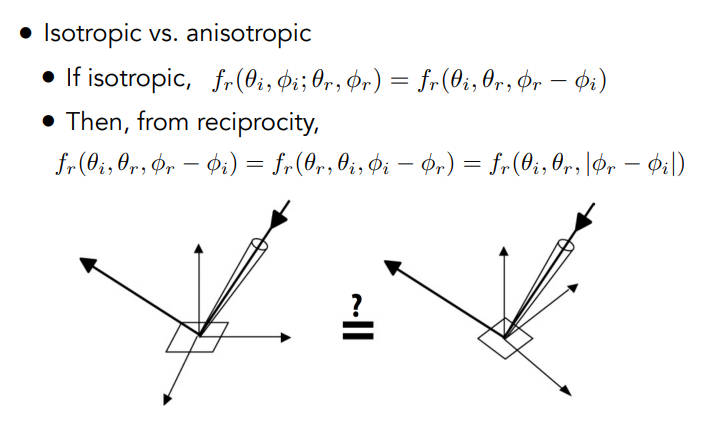
- 各向异性定义:如果入射出射角不变,只有方位角旋转,看到的BRDF不一样那就是各向异性的材质,反之如果一样就是各向同性的材质
Anisotropic Brushed Metal
Anisotropic BRDF: Nylon
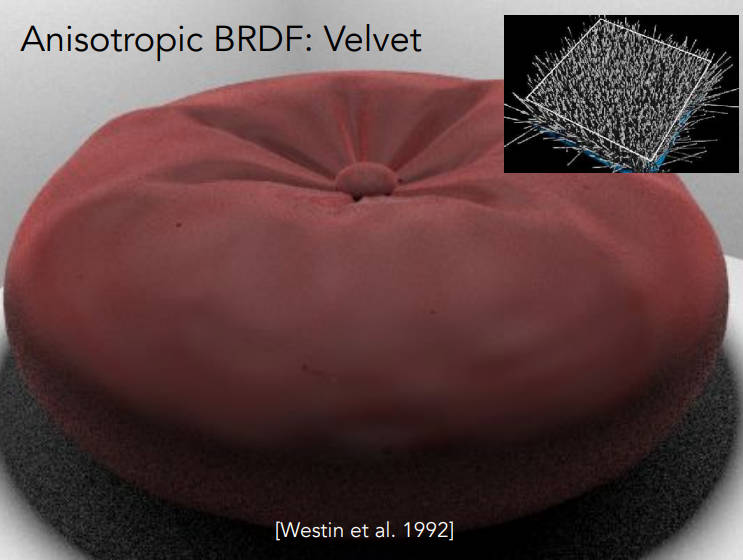
Anisotropic BRDF: Velvet
Properties of BRDFs
非负,他表示的是能量的分布
线性分布,可以拆成很多块,然后加起来
可逆性,入射方向和出射方向调换得到的brdf一模一样
能量守恒,能量不可能变多
各向同性和各向异性
- 如果是各项同性的材质,维度降低了一维
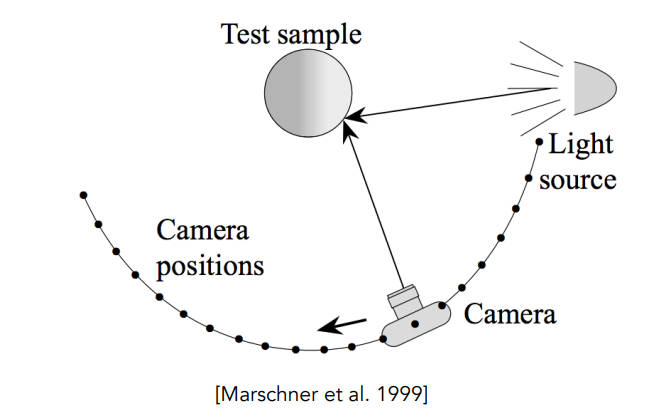
Measuring BRDFs
Image-Based gonioreflectometer
- 枚举所有的出射方向和入射方向进行测量
提升效率的一些方法
各向同性降维
可逆性,砍半
采样若干点后其他点进行猜测
Representing Measuring BRDFs
- Tabular Representing