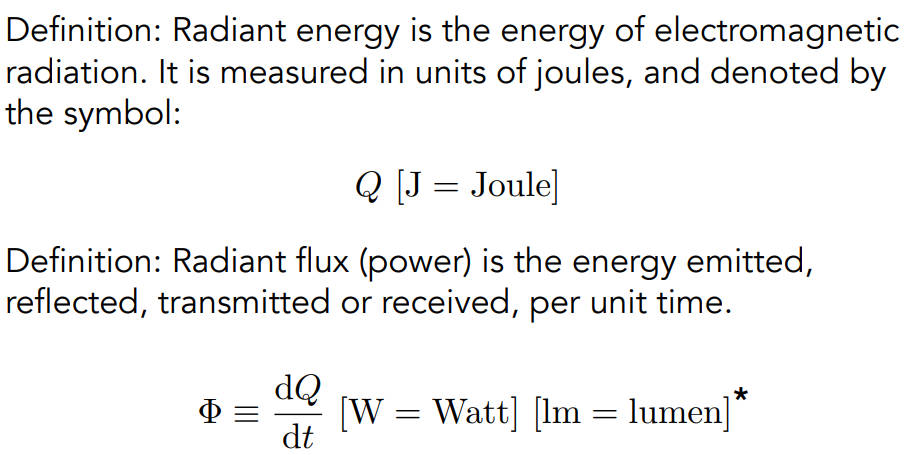Using AABBs to accelerate ray tracing
Uniform grids
主旨:多做光线与盒子求交
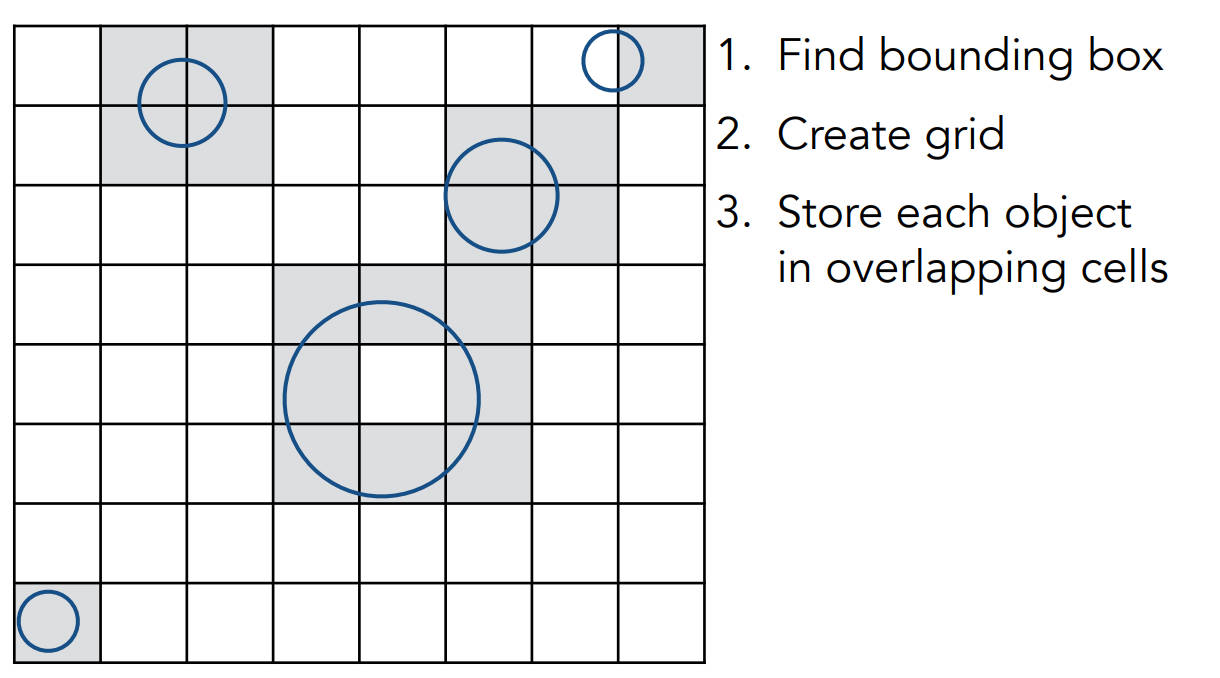
先把场景的BB框住,然后在BB里创建格子
记录每个有物体(表面)存在的格子(下图中右上角少画了一个格子)
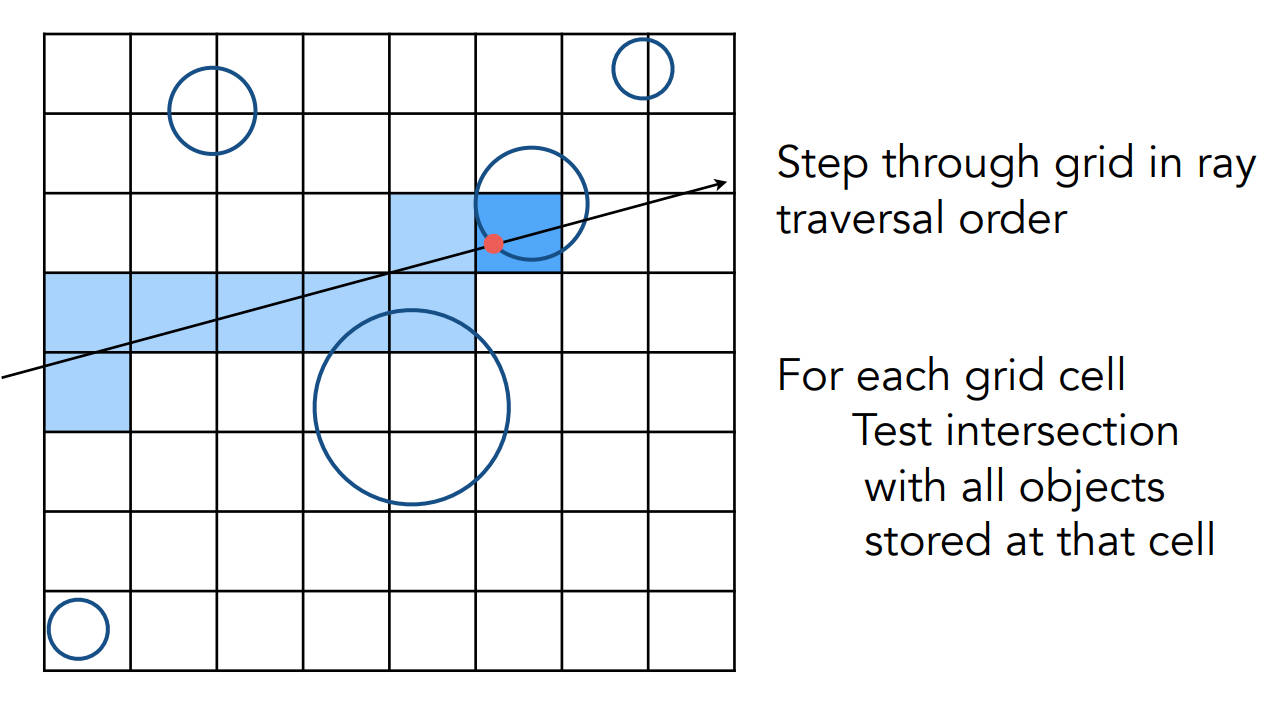
判断跟光线相交的格子里有没有物体
如果有物体,那么说明光线可能和该物体相交,就计算交点
在光线的发射过程中(对于图中的光线),只需判断当前格子的上方和右方是否为光线下一个相交的格子
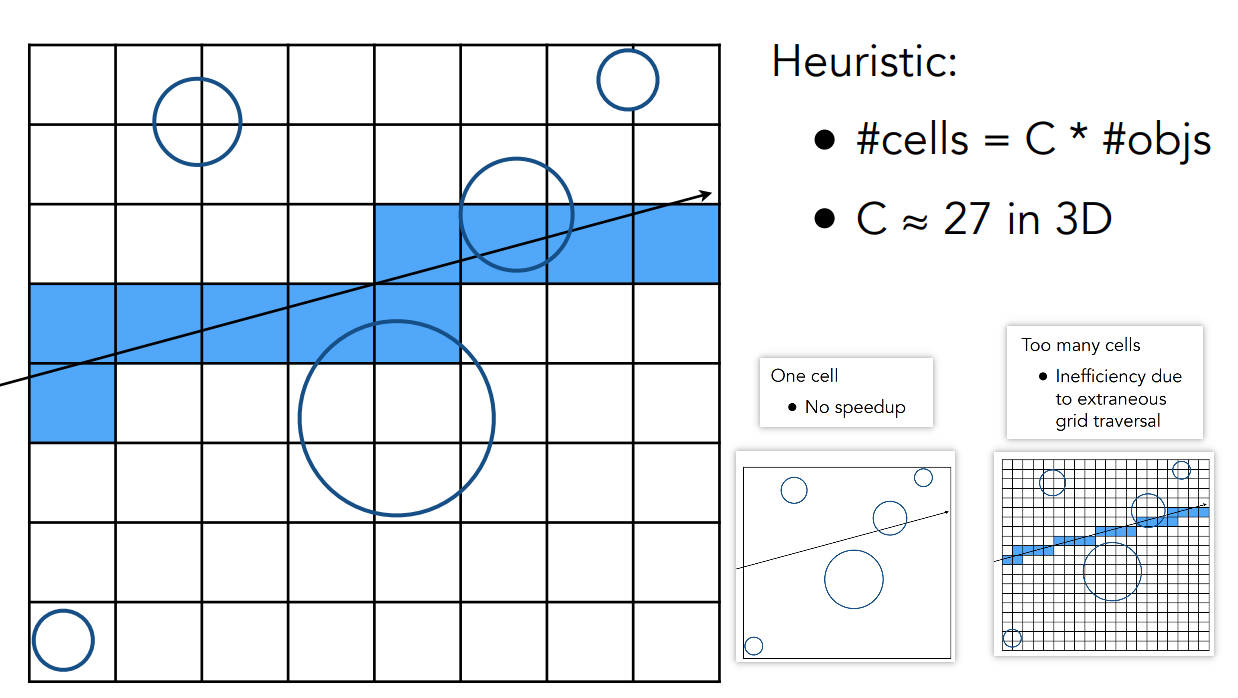
Grid Resolution
- 不能太稀疏(比如1*1*1的格子,相当于没做BBAA),也不能太密集,不然和格子也求交太多次,所以要有一个均衡
- BBAA适合比较均匀的场景,不适合有大片空区域的场景,会产生“Teapot in a stadium”问题
Spatial partitions(空间划分)
基于格子的不足之处进行优化,在物体分布稀疏的地方格子大一点,,分布密集的地方格子小一点
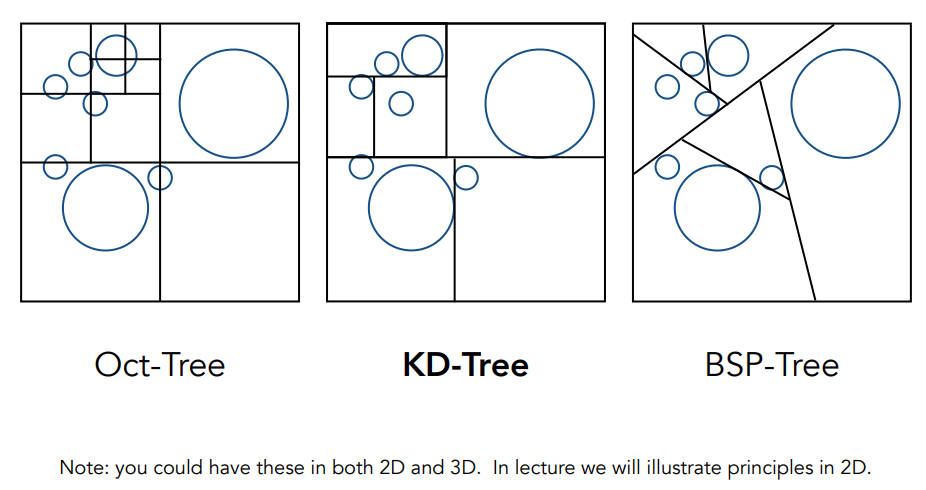
八叉树(Oct-Tree),对空间切三刀,然后如果某个小空间中物体比较多,继续切,直到空间内没物体或者物体数量差不多了,但维度再高的话,就是$2^n$叉树,这显然不好(我认为老师意思是说这么切下去还是切太多了),为解决这个问题,KD-Tree应运而生
KD-Tree:每次砍一刀,然后再根据情况在分出的一个空间内再砍一刀,这样就类似二叉树,每次水平一刀,竖直一刀,这样划分的相对均匀一点
BSP-Tree:不是横平竖直地砍,所以比较复杂
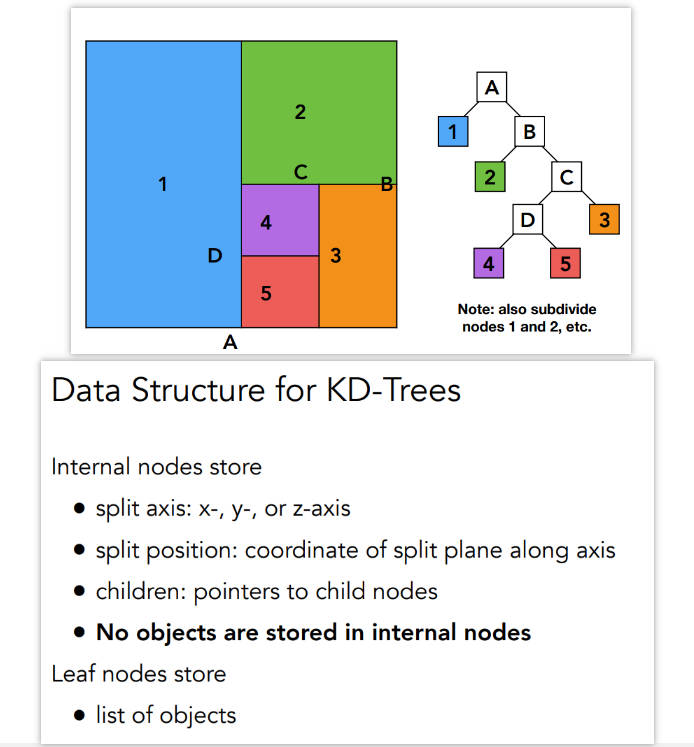
KD-Tree Pre-Processing
- 在做光追之前提前划分好,在中间节点记录它之后划分了什么样的格子,在叶子节点来实际存储和格子相交的物体(三角形)
首先,光线和整个BBAA*(A)有交点,那么对于子节点(也就是1和B)都判断是否有交点
都相交,但1也就到此为止,去计算1中所有物体是否与光线相交,然后去计算B的子节点2和C
还是都相交,但2也到此为止,去计算2中所有物体是否与光线相交,然后去计算C的子节点3和D
还是都相交,继续算
到4和5,其中5是没有交点的,所以就不计算了
有几个问题:
如何判断包围盒的格子到底和哪些三角形相交,这个问题比较困难处理
一个物体与多个包围盒相交,也就是多个叶子节点都要储存该物体
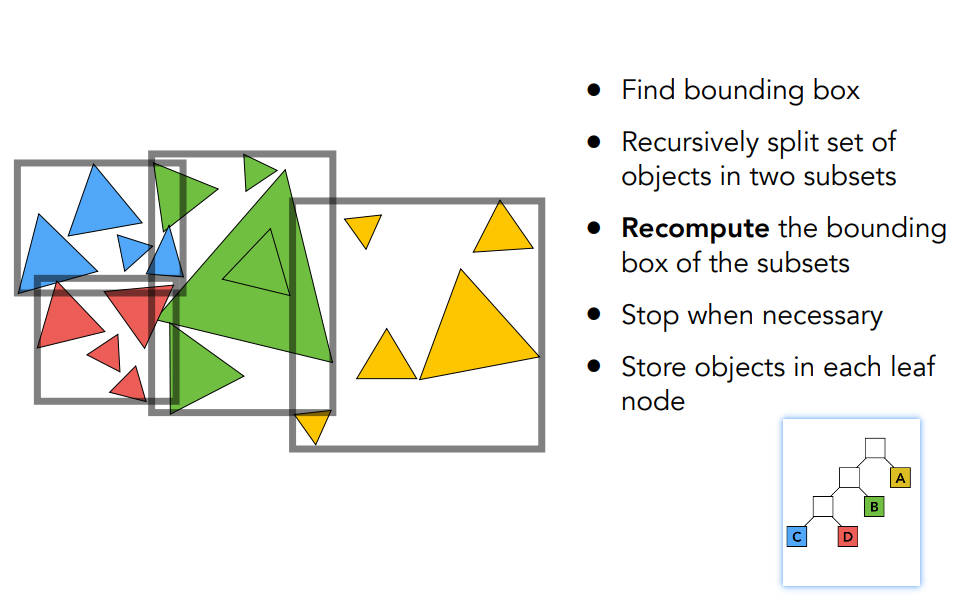
Object Partitions & Bounding Volume Hierarchy(BVH)
解决了KD-Tree的两个问题,既不用求交,而且一个三角形不会与多个包围盒相交,只会存在一个包围盒中
但问题是包围盒有可能相交,怎么划分很讲究
怎样区分一个节点:
选择一个维度去划分(x、y、z轴)
总是沿着最长的轴去切
区分节点(切)的时候,从中间物体的位置切,快速找出中位数,使用快速选择算法,只需要O(n)的复杂度
如果是动态场景,就需要重新计算BVH了
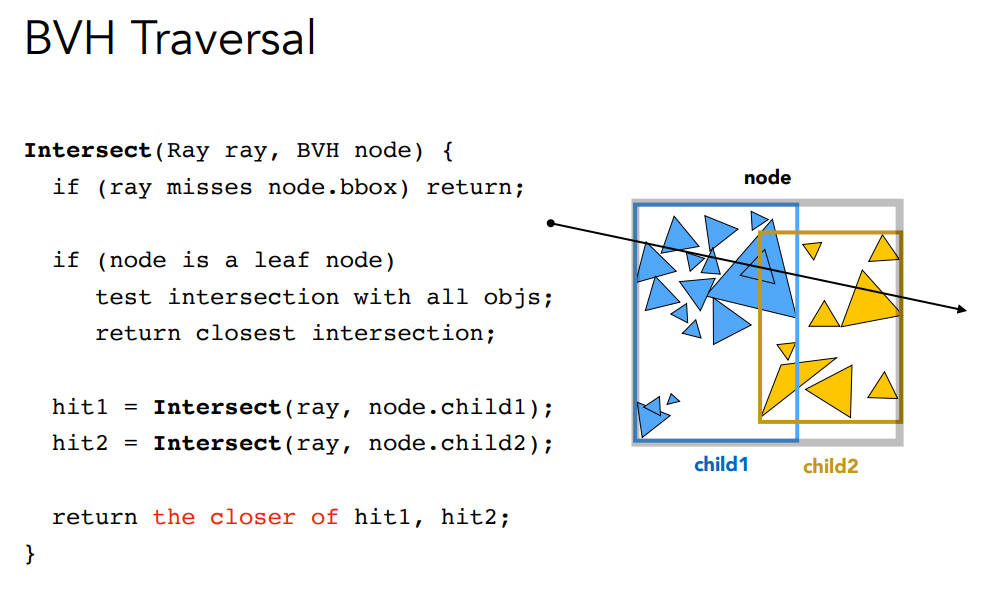
BVH伪代码:
Spatial VS Object Partitions
空间划分和物体划分的区别
空间:
划分了不重叠的空间区域
一个物体可能会被包含在多个空间中
物体:
物体被划分到不同的子集中
包围盒可能会重叠
Basic radiometry (辐射度量学)
Motivation
为光赋予物理意义
定义了一些列的方法和单位来描述光照
准确计量光在空间中的各种属性
Radiant flux:光通量,单位时间内通过的光总量,单位watt或者lumen(lm)
intensity:光强,单位立方角光通量,单位Watt/steradians,也就是candelas
irradiance:辉度,单位面积光通量,瓦特/平方米
radiance:光亮度
Radiant Energy and Flux(Power)
Radiant Energy:可以理解为光的能量,单位是焦耳
Radiant Flux(power):单位时间的能量,单位是瓦特
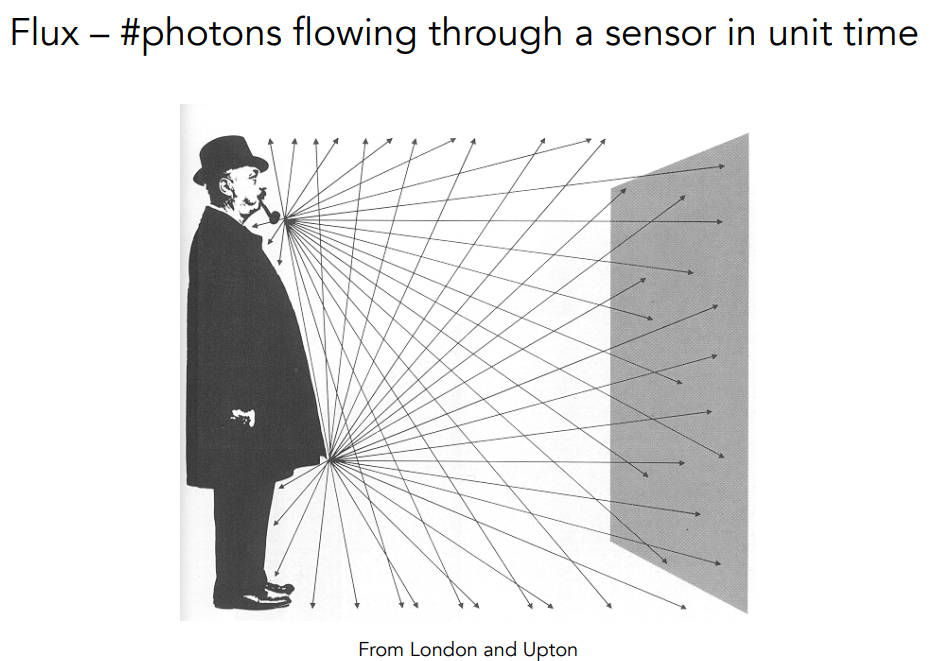
Flux(另外一种解释):光打到一个感光的平面,单位时间内通过的光子的数量
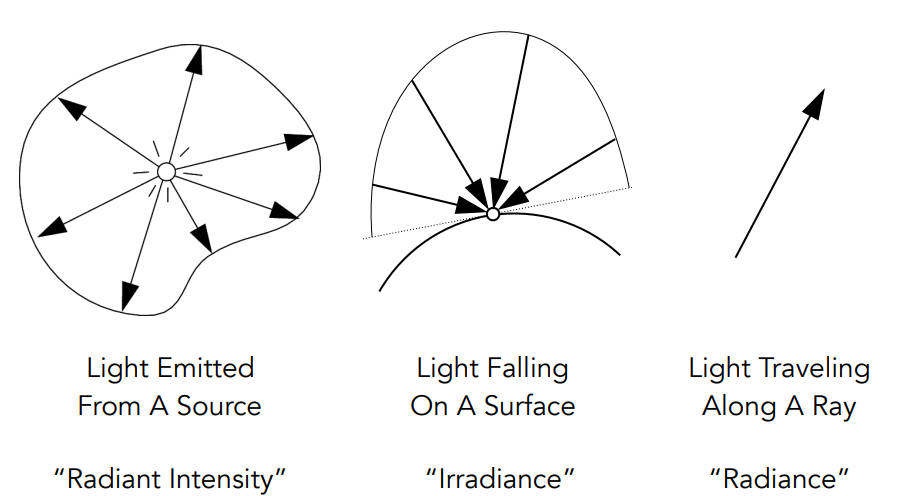
Important Light Measurements of Interest
Radiant Intensity:光源散发的光
irradiance:一个平面接收的光
radiance:在传播中的光
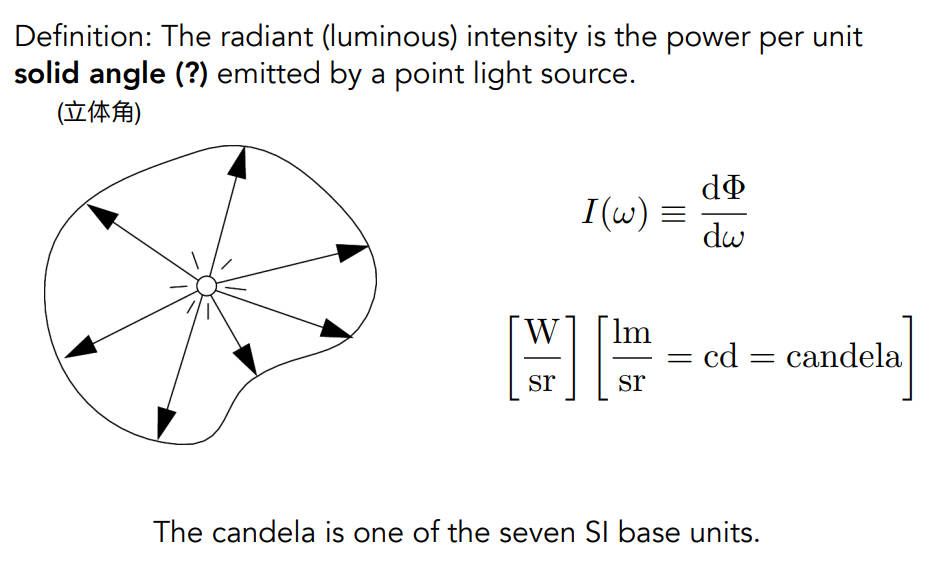
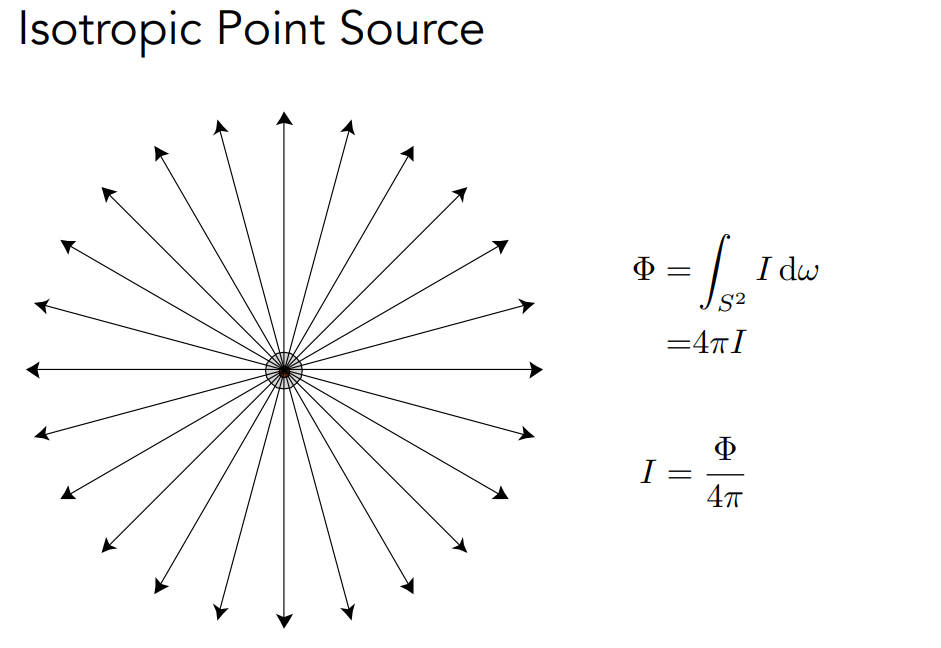
Radiant Intensity
- 单位立体角的能量
二维中角度一般指弧度,单位是radians
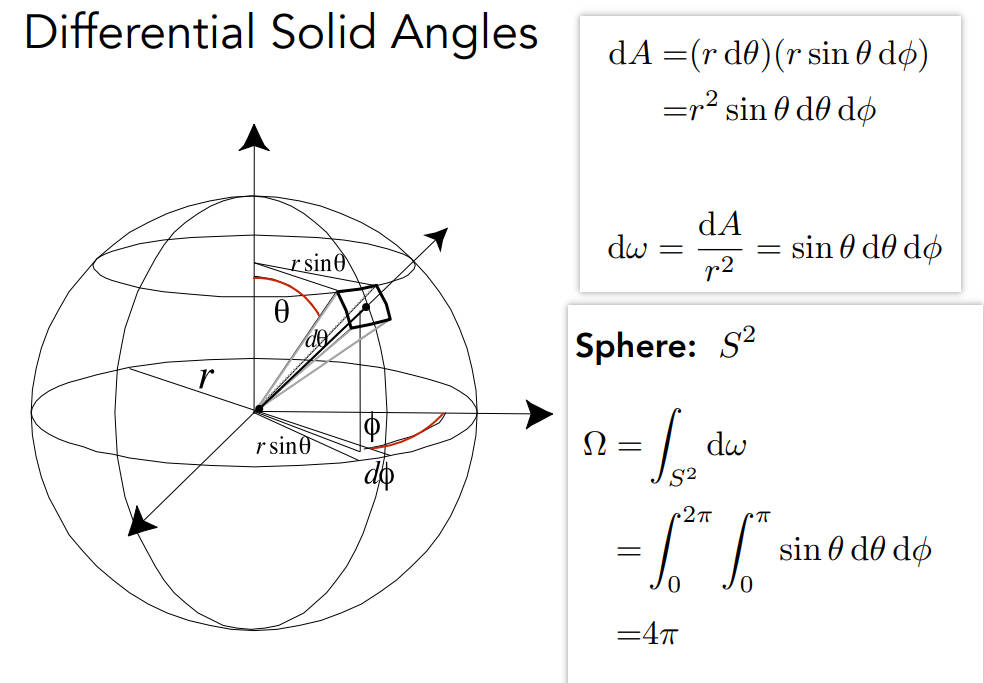
三维中立体角:球上一块面积除以半径的平方,球有$4\pi$的立体角,单位是steradians
- 单位立体角/微分立体角:微分面积/半径平方
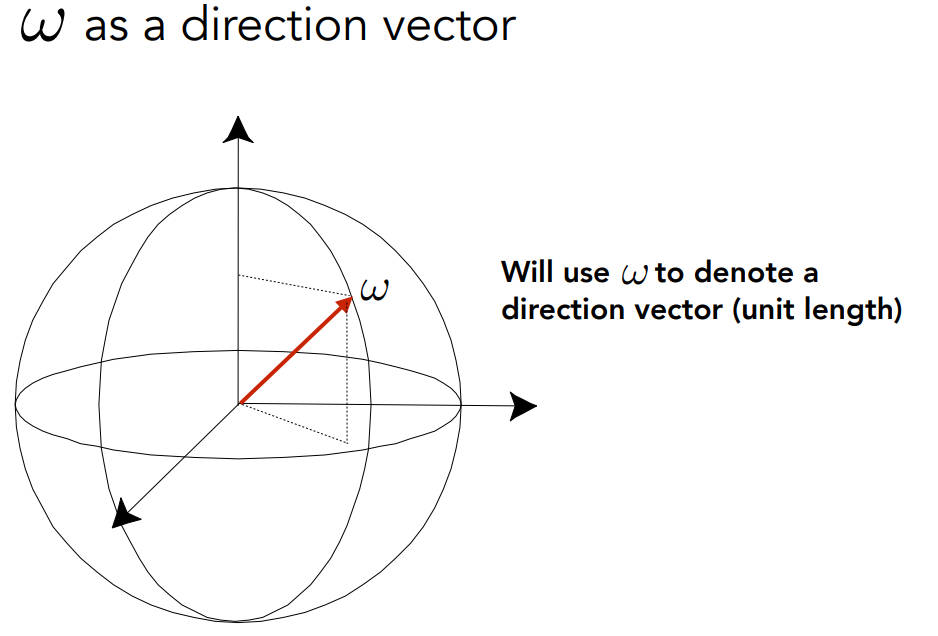
- 之后会用单位立体角w来表示一个单位向量
- Radiant Intensity就是单位立体角的能量
作业6
在之前的编程练习中,我们实现了基础的光线追踪算法,具体而言是光线传
输、光线与三角形求交。我们采用了这样的方法寻找光线与场景的交点:遍历场景
中的所有物体,判断光线是否与它相交。在场景中的物体数量不大时,该做法可以
取得良好的结果,但当物体数量增多、模型变得更加复杂,该做法将会变得非常低
效。因此,我们需要加速结构来加速求交过程。在本次练习中,我们重点关注物体
划分算法 Bounding Volume Hierarchy (BVH)。本练习要求你实现 Ray-Bounding
Volume 求交与 BVH 查找。
首先,你需要从上一次编程练习中引用以下函数:
Render() in Renderer.cpp: 将你的光线生成过程粘贴到此处,并且按照新框架更新相应调用的格式。
Triangle::getIntersection in Triangle.hpp: 将你的光线-三角形相交函数粘贴到此处,并且按照新框架更新相应相交信息的格式。
在本次编程练习中,你需要实现以下函数:
IntersectP(const Ray& ray, const Vector3f& invDir,const std::array<int, 3>& dirIsNeg) in the Bounds3.hpp: 这个函数的作用是判断包围盒 BoundingBox 与光线是否相交,你需要按照课程介绍的算法实现求交过程。
getIntersection(BVHBuildNode* node, const Ray ray)in BVH.cpp: 建立 BVH 之后,我们可以用它加速求交过程。该过程递归进行,你将在其中调用你实现的 Bounds3::IntersectP
Render()函数
其实render函数已经写的差不多了,计算投射的光线已经算出来了,只需要再写一行代码调用函数即可,需要调用的是Scene类的castRay函数,与上一次作业不同,这次作业的形参做了修改,需要直接传入ray对象,至于深度depth,不用管,就是记录个射线的弹射次数,填0即可
framebuffer[m++] = scene.castRay(ray, 0);,加这行代码即可,完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
void Renderer::Render(const Scene& scene)
{
std::vector<Vector3f> framebuffer(scene.width * scene.height);
float scale = tan(deg2rad(scene.fov * 0.5));
float imageAspectRatio = scene.width / (float)scene.height;
Vector3f eye_pos(-1, 5, 10);
int m = 0;
for (uint32_t j = 0; j < scene.height; ++j) {
for (uint32_t i = 0; i < scene.width; ++i) {
// generate primary ray direction
float x = (2 * (i + 0.5) / (float)scene.width - 1) *
imageAspectRatio * scale;
float y = (1 - 2 * (j + 0.5) / (float)scene.height) * scale;
// TODO: Find the x and y positions of the current pixel to get the
// direction
// vector that passes through it.
// Also, don't forget to multiply both of them with the variable
// *scale*, and x (horizontal) variable with the *imageAspectRatio*
// Don't forget to normalize this direction!
Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
dir = normalize(dir);
Ray ray(eye_pos, dir);
framebuffer[m++] = scene.castRay(ray, 0);
}
UpdateProgress(j / (float)scene.height);
}
UpdateProgress(1.f);
// save framebuffer to file
FILE* fp = fopen("binary.ppm", "wb");
(void)fprintf(fp, "P6\n%d %d\n255\n", scene.width, scene.height);
for (auto i = 0; i < scene.height * scene.width; ++i) {
static unsigned char color[3];
color[0] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].x));
color[1] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].y));
color[2] = (unsigned char)(255 * clamp(0, 1, framebuffer[i].z));
fwrite(color, 1, 3, fp);
}
fclose(fp);
}
Triangle::getIntersection函数
- 这个部分说难吧也不难,说简单吧,倒也不好想,基本的算法已经是算完了,主要就是把算好的内容返回,那么返回的是一个Intersection对象,所以就需要了解下Intersection类,需要根据这个函数的计算结果来创建好要返回的Intersection对象,完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
inline Intersection Triangle::getIntersection(Ray ray)
{
Intersection inter;
if (dotProduct(ray.direction, normal) > 0)
return inter;
double u, v, t_tmp = 0;
//下面的代码已经是Moller Trumbore Algorithm了
Vector3f pvec = crossProduct(ray.direction, e2);//该向量与三角形法线正交
double det = dotProduct(e1, pvec);//det 的几何意义是三角形两个边向量以及光线方向向量构成的三维矩阵的行列式。
if (fabs(det) < EPSILON)//如果det接近0,说明两个边向量接近平行,从而导致三角形面积接近0,即三角形退化为线段或点
return inter;
double det_inv = 1. / det;
Vector3f tvec = ray.origin - v0;
u = dotProduct(tvec, pvec) * det_inv;
if (u < 0 || u > 1)
return inter;
Vector3f qvec = crossProduct(tvec, e1);
v = dotProduct(ray.direction, qvec) * det_inv;
if (v < 0 || u + v > 1)
return inter;
t_tmp = dotProduct(e2, qvec) * det_inv;
// TODO find ray triangle intersection
if (t_tmp < 0) return inter;
inter.happened = true;//是否相交
inter.coords = ray(t_tmp);//交点坐标
inter.normal = normal;//交点处三角形法线
inter.distance = t_tmp;//d
inter.obj = this;//三角形
inter.m = m;//交点处三角形的材质
return inter;
}
IntersectP函数
- 其实这个就按课程上讲的过程来算就行了,算出光线进入时间和推出时间即可,我看有的博主使用vector相乘,规避了for循环,这点还是很不错的。有一个点让人比较费解,就是IntersectP函数的形参中有一个是
const std::array<int, 3>& dirIsNeg,实际上我全程没用到这个函数。我的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
const std::array<int, 3>& dirIsNeg) const
{
// invDir: ray direction(x,y,z), invDir=(1.0/x,1.0/y,1.0/z), use this because Multiply is faster that Division
// dirIsNeg: ray direction(x,y,z), dirIsNeg=[int(x>0),int(y>0),int(z>0)], use this to simplify your logic
// TODO test if ray bound intersects
double t_enter, t_exit;
double t_min[3]{}, t_max[3]{};
for (int i = 0; i < 3; i++)
{
t_min[i] = std::min((pMin[i] - ray.origin[i]) * invDir[i], (pMax[i] - ray.origin[i]) * invDir[i]);
t_max[i] = std::max((pMin[i] - ray.origin[i]) * invDir[i], (pMax[i] - ray.origin[i]) * invDir[i]);
}
t_enter = std::fmax(t_min[0], std::fmax(t_min[1],t_min[2]));
t_exit = std::fmin(t_max[0], std::fmin(t_max[1], t_max[2]));
if (t_enter < t_exit && t_exit >= 0.0) return true;
return false;
}
getIntersection函数
- 这个函数就照着课程ppt的伪码来做就行了,有几点让人费解,就是上面说的参数,有一个我就没用,还有就是光线方向的倒数,这个直接在ray对象那取出来就好,不用自己算,我一开始还在想怎么算,万一除以个0该怎么处理,实际上在ray的构造函数里就自己算了,而且就是简单的除以,没考虑除以0的情况,呃呃。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Intersection BVHAccel::getIntersection(BVHBuildNode* node, const Ray& ray) const
{
// TODO Traverse the BVH to find intersection
Intersection inter;
if (!node || !node->bounds.IntersectP(ray, ray.direction_inv, { 0,0,0 }))
return inter;
if (node->left == nullptr && node->right == nullptr)
{
return node->object->getIntersection(ray);
}
Intersection inter1 = getIntersection(node -> left, ray);
Intersection inter2 = getIntersection(node->right, ray);
return inter1.distance < inter2.distance ? inter1 : inter2;
}
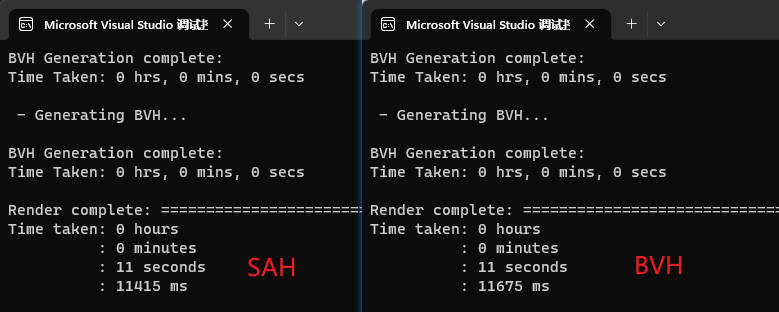
提高题:SAH
这个sah我搞了不少时间才弄懂,但就结果而言,提升并不是很高,具体过程我就不多赘述了,我挂两个我参考的链接,我在代码处有一些注释
BVH with SAH (Bounding Volume Hierarchy with Surface Area Heuristic) - lookof - 博客园 (cnblogs.com)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
BVHBuildNode* BVHAccel::recursiveBuild(std::vector<Object*> objects)
{
BVHBuildNode* node = new BVHBuildNode();
// Compute bounds of all primitives in BVH node
Bounds3 bounds;
for (int i = 0; i < objects.size(); ++i)
bounds = Union(bounds, objects[i]->getBounds());
if (objects.size() == 1) {
// Create leaf _BVHBuildNode_
node->bounds = objects[0]->getBounds();
node->object = objects[0];
node->left = nullptr;
node->right = nullptr;
return node;
}
else if (objects.size() == 2) {
node->left = recursiveBuild(std::vector{objects[0]});
node->right = recursiveBuild(std::vector{objects[1]});
node->bounds = Union(node->left->bounds, node->right->bounds);
return node;
}
else {
Bounds3 centroidBounds;
for (int i = 0; i < objects.size(); ++i)
centroidBounds =
Union(centroidBounds, objects[i]->getBounds().Centroid());
int dim = centroidBounds.maxExtent();
SplitMethod splitMethod = SplitMethod::NAIVE;
switch (splitMethod)
{
case SplitMethod::SAH :
{
const int nBuckets = 12;
const float SAHTravCost = 0.125f;//遍历花费的时间成本
//const float SAHInterCost = 1.f;//检查一个物体花费的时间成本,其实可以不算
BucketInfo buckets[nBuckets];
//遍历三角形,查看三角形的质心位于哪一个桶中
for (int i = 0; i < objects.size(); i++)
{
//用来存当前图元也就是三角形质心位于几号桶中,dim是最松散的一个轴
int b = nBuckets * centroidBounds.Offset(objects[i]->getBounds().Centroid())[dim];
if (b == nBuckets) b = nBuckets - 1;
buckets[b].count++;
buckets[b].bounds = Union(buckets[b].bounds, objects[i]->getBounds());
}
//下面计算最小成本
float cost[nBuckets - 1]{ 0.f };
//按i的序号,将桶分成两部分,所以不取最后一个桶
//因为如果左边取了最后一个桶,那么相当于右边没有桶了,这也是为啥cost数组长度为nBuckets - 1
for (int i = 0; i < nBuckets - 1; i++)
{
Bounds3 b0, b1;
int cnt0 = 0, cnt1 = 0;
for (int j = 0; j <= i; j++)
{
b0 = Union(b0, buckets[j].bounds);
cnt0++;
}
for (int j = i + 1; j <= nBuckets - 1; j++)
{
b1 = Union(b1, buckets[j].bounds);
cnt1++;
}
cost[i] = SAHTravCost + (cnt0 * b0.SurfaceArea() + cnt1 * b1.SurfaceArea() ) / bounds.SurfaceArea();
}
//找出最小时间成本的划分桶序号
//船新的找最小值下标方法,一行代码解决
int minCostSplitBucket = std::distance(cost, std::min_element(cost, cost + nBuckets - 1));
//下面是传统的找最小值方法
float minCost = cost[0];
for (int i = 1; i < nBuckets - 1; i++)
{
if (cost[i] < minCost)
{
minCost = cost[i];
minCostSplitBucket = i;
}
}
float leafCost = objects.size();//直接将当前所有图元也就是三角形都检测一遍的时间成本
//如果当前图元数量大于一个节点允许的最大图元数量,那就需要按桶序号来划分两个区域
//或者使用区域划分的时间成本确实小于将当前图元不划分的时间成本,那也要划分
//但这个maxPrimsInNode设置为1.所以都会执行这段代码,甚至size为2的时候都轮不到执行这块代码
if (objects.size() > maxPrimsInNode || minCost < leafCost)
{
auto pmid = std::partition(objects.begin(), objects.end(), [=](Object* pi){
int b = nBuckets * centroidBounds.Offset(pi->getBounds().Centroid())[dim];
if (b == nBuckets) b = nBuckets - 1;
return b <= minCostSplitBucket;
});
auto beginning = objects.begin();
auto ending = objects.end();
auto leftshapes = std::vector<Object*>(beginning, pmid);
auto rightshapes = std::vector<Object*>(pmid, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
node->left = recursiveBuild(leftshapes);
node->right = recursiveBuild(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
break;
}
//如果这个划分效果还不如直接算,那就不break,直接执行下面的的
//但是我的maxPrimsInNode设置的是1,所以无论如何都用sah,所以就先break下
break;
}
case SplitMethod::NAIVE :
{ switch (dim) {
case 0:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().x <
f2->getBounds().Centroid().x;
});
break;
case 1:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().y <
f2->getBounds().Centroid().y;
});
break;
case 2:
std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
return f1->getBounds().Centroid().z <
f2->getBounds().Centroid().z;
});
break;
}
auto beginning = objects.begin();
auto middling = objects.begin() + (objects.size() / 2);
auto ending = objects.end();
auto leftshapes = std::vector<Object*>(beginning, middling);
auto rightshapes = std::vector<Object*>(middling, ending);
assert(objects.size() == (leftshapes.size() + rightshapes.size()));
node->left = recursiveBuild(leftshapes);
node->right = recursiveBuild(rightshapes);
node->bounds = Union(node->left->bounds, node->right->bounds);
break;
}
}
}
return node;
}