GAMES101-Lecture 13 Ray Tracing 1(Whitted-Style Ray Tracing) & 作业5

Why Ray Tracing

光栅化不能解决全局的效果
- 软阴影
- Glossy reflection（光泽度反射）（打磨的比较光滑的金属，类似古代的铜镜）
- 间接光照
光追准确但很慢
- 光栅化：实时；光追：离线（一帧需要一万个gpu小时）

Basic Ray-Tracing Algorithm

Light Rays(假设的条件)

光线沿着直线传播
光线和光线不会发生碰撞
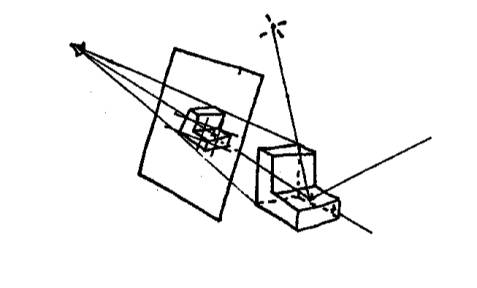
光线从光源发射最后弹到眼睛里，而且光路可逆

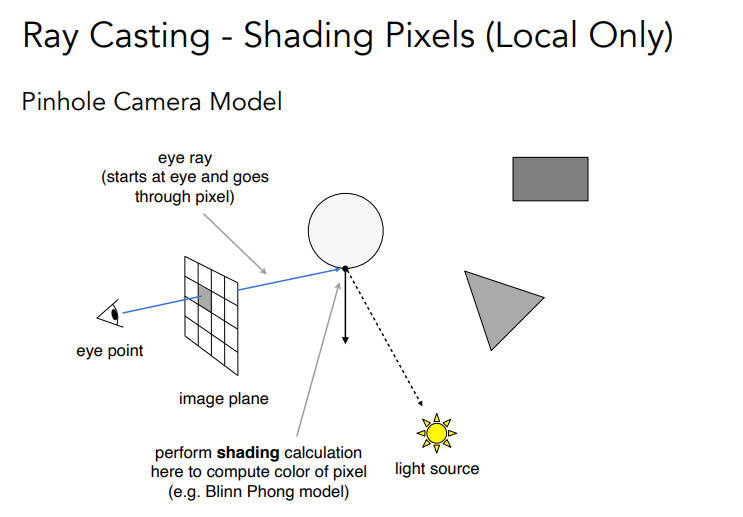
Ray Casting

通过从摄像机投射每一个像素来生成一张图
检查投射到的物体上的点，连接光源，判断是不是在阴影

其实这种效果和光栅化很相似，并没有弹射，只是不需要z-buffer了

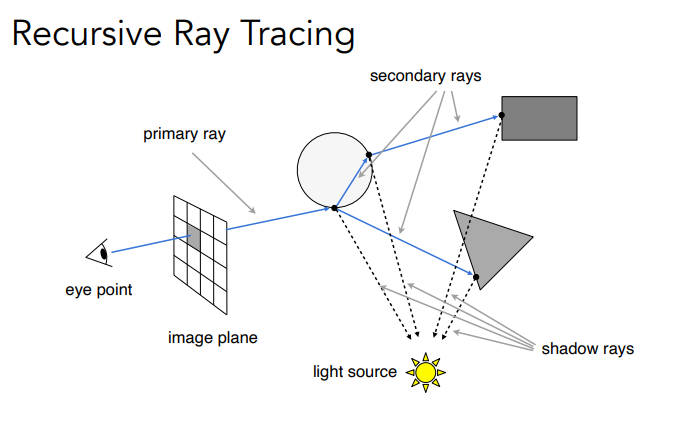
Recursive（Whitted-Style）Ray Tracing

可以进行多次弹射（反射、折射）
在每一个弹射的点都与光源连接，判断是不是在阴影，然后把不在阴影的颜色加起来
弹射的过程有能量损失，不然就过曝了

Ray-Surface Intersection

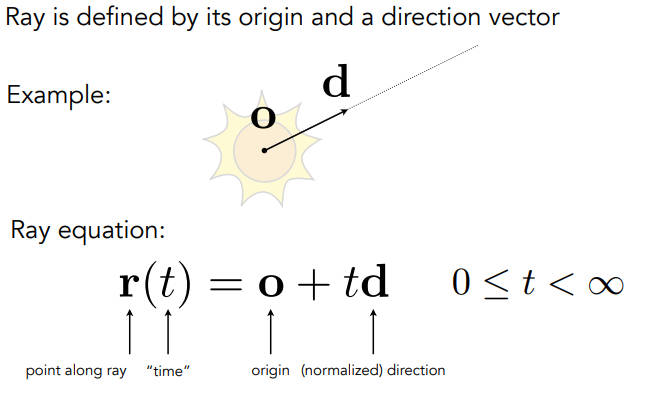
Ray Equation

光线就是光源+一个方向向量
光线r在t时间从一个起点到一个方向的位置

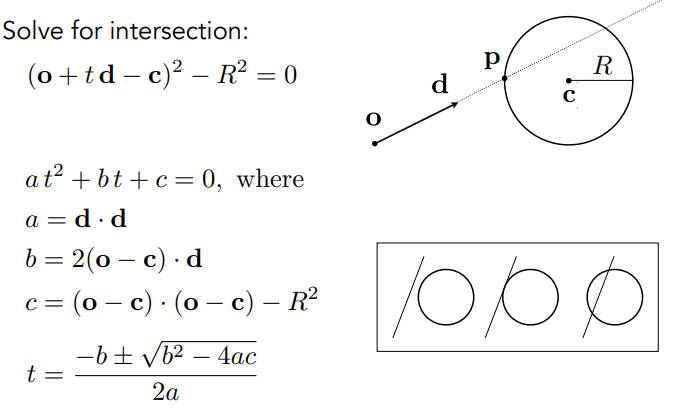
Ray Intersection With Sphere(Implicit Surface)

点p是球上一点满足o+td，求t（二次函数）
需要满足实际意义，所以t得是正的，而且是个实数
相交时，要取更近的，取更小的t

按这个方法，隐式表面就很好算了

Ray Intersection With Triangle Mesh(emplicit Surface)

可以判断一个点在物体内还是物体外，从点开始往任意一个方向发射一根射线，如果与物体的交点是奇数个，那么就说明在物体内（物体得是封闭的）
最普通的方法是遍历物体所有的三角形，来看看到底和哪个三角形相交了，找出最近的点，但速度会非常慢
那么如何计算和三角形的交点，分解成两个问题：
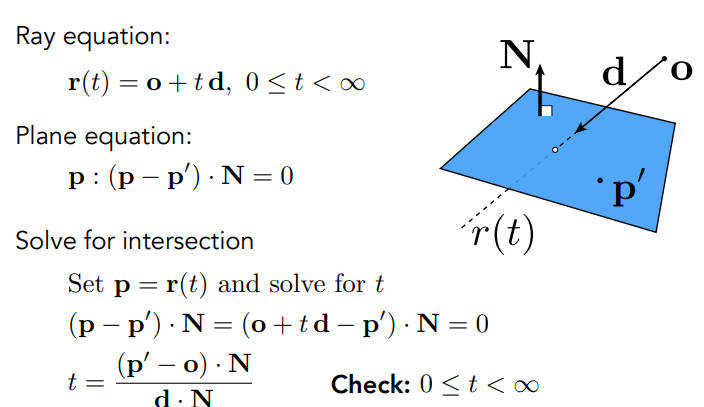
- 光线和平面求交（根据三角形的属性计算出三角形所在的平面）
- 找到交点后判断是否在三角形内
平面被定义为一个方向（法线）和一个点，满足下图公式的点p，就在平面上，平面就是一些列p点的集合

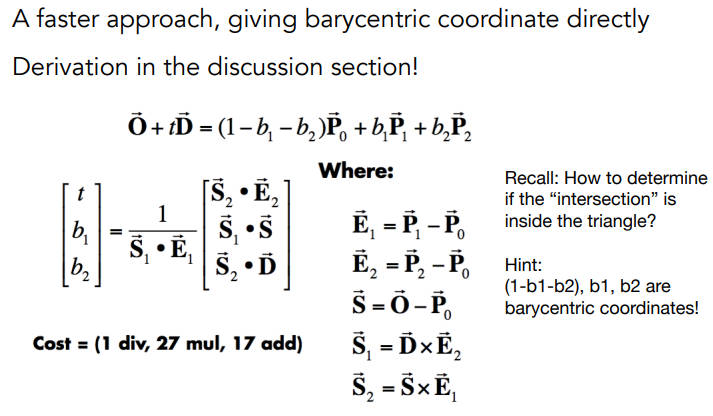
Moller Trumbore Algorithm

在上述式子中，右侧是使用重心坐标求得三角形p0p1p2平面的一个点，左侧是光线要交的点，只要通过式子求出t即可，那么点都是三维的，所以就是三个方程三个未知量（t、b1、b2）
解出b1、b2、1-b1-b2都是非负的，那就在三角形内
这样就可以直接求出光线是否和三角形有交点，但实际上本质还是先看是不是交在了三角形所在的平面上

Accelerating Ray-Surface Intersection

Bouding Volumes(包围体积)

逻辑：如果光线和包围盒都不相交，那么更不可能和里面的物体相交
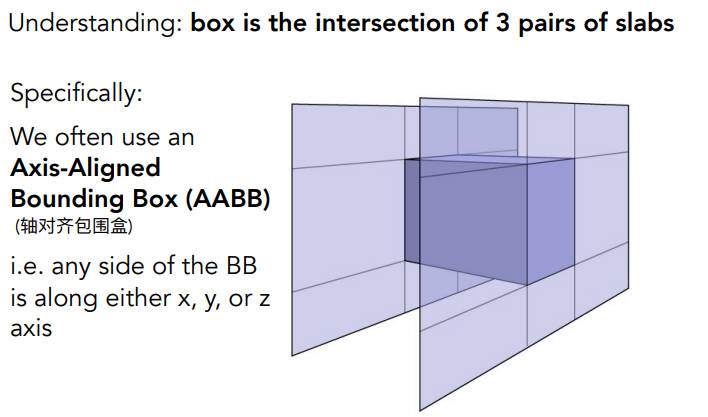
包围盒：三个对面形成的交集
长方体的每个轴沿着坐标轴，叫轴对齐包围盒

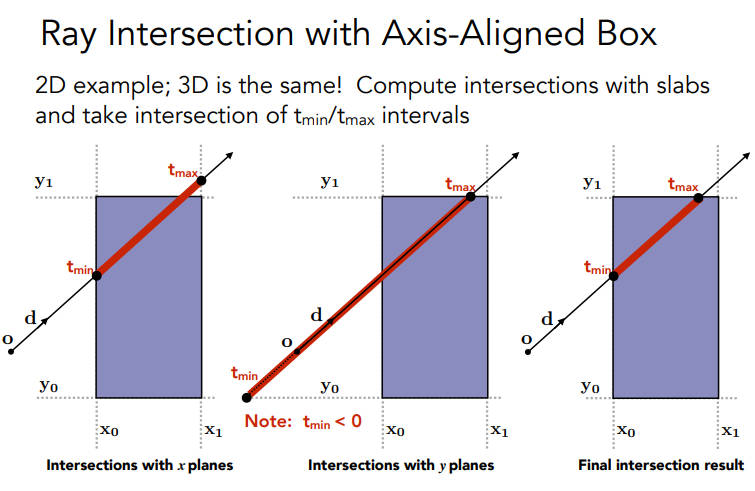
先把情况降维，算光线和二维的BB相交的情况
首先算和两条个平面的两个交点对应的tmin和tmax，再算出和两个y平面的交点所对应的tmin和tmax，然后求个交集，也就得到了光线穿过BB时的tmin和tmax

那么对于三维的BB来说，只有：
- 当光线进入三对面时才算进入了BB
- 当光线只要退出了一对面就算出了BB
先计算光线对于每一对面的$t_{min}$和$t_{max}$
$t_{enter} = max{t_{min}},t_{exit} = min{t_{max}}$
如果$t_{enter}<t_{exit}$，那么说明光线在这个BB里存在了一段时间，反之则没有穿过BB
如果$t_{exit}<0$，说明盒子一定在光线的背后
如果$t_{exit}>=0$且$t_{enter}<0$，说明光线的起点在盒子中
总之，光线和AABB相交当且仅当$t_{enter}<t_{exit} \&\& t_{exit}>=0$
为什么要axis-aligned呢
- 为了使计算相对容易

作业5

题目要求：
- 在这部分的课程中，我们将专注于使用光线追踪来渲染图像。在光线追踪中
最重要的操作之一就是找到光线与物体的交点。一旦找到光线与物体的交点，就
可以执行着色并返回像素颜色。在这次作业中，我们需要实现两个部分：光线的
生成和光线与三角的相交。本次代码框架的工作流程为：
1. 从 main 函数开始。我们定义场景的参数，添加物体（球体或三角形）到场景
中，并设置其材质，然后将光源添加到场景中。
1. 调用 Render(scene) 函数。在遍历所有像素的循环里，生成对应的光线并将
返回的颜色保存在帧缓冲区（framebuffer）中。在渲染过程结束后，帧缓冲
区中的信息将被保存为图像。
1. 在生成像素对应的光线后，我们调用 CastRay 函数，该函数调用 trace 来
查询光线与场景中最近的对象的交点。
1. 然后，我们在此交点执行着色。我们设置了三种不同的着色情况，并且已经
为你提供了代码。
你需要修改的函数是：
- Renderer.cpp 中的 Render()：这里你需要为每个像素生成一条对应的光
线，然后调用函数 castRay() 来得到颜色，最后将颜色存储在帧缓冲区的相
应像素中。
- Triangle.hpp 中的 rayTriangleIntersect(): v0, v1, v2 是三角形的三个
顶点，orig 是光线的起点，dir 是光线单位化的方向向量。tnear, u, v 是你需
要使用我们课上推导的 Moller-Trumbore 算法来更新的参数。
第一，是第一个生成光线，这个需要找到每个像素的世界坐标，而这个过程是从像素坐标->NDC坐标->Screen坐标->世界坐标，在课程中并没有详细地讲，但其实在光栅化的时候说过。可是我还是不清楚，所以参考了博客光线追踪：生成相机光线 (scratchapixel.com)
只需要在Render函数的注释下面算出dir的x和y即可

  
    for (int j = 0; j < scene.height; ++j)
    {
        for (int i = 0; i < scene.width; ++i)
        {
            // generate primary ray direction
            float x;
            float y;
            // TODO: Find the x and y positions of the current pixel to get the direction
            // vector that passes through it.
            // Also, don't forget to multiply both of them with the variable *scale*, and
            // x (horizontal) variable with the *imageAspectRatio*            
            //这个地方的细节在课程中并没有提及，所以还是得查
            //目标是将屏幕上的像素转换为世界坐标中
            //首先先将像素转换到NDC空间中
            x = ((float)i + 0.5f) / scene.width;
            y = ((float)j + 0.5f) / scene.height;
            //再将x，y转换到screen空间中
            x = 2 * x - 1.f;
            y = -(2 * y - 1.f);//y轴方向向下，所以取个负值
            //然后现在的坐标是在正方形中的坐标，要根据宽高比拉伸一下
            x *= imageAspectRatio;
            //最后是计算在世界坐标系中的像素坐标,其实应该乘以相机到平面的距离，但是默认都是1，所以不用乘
            x *= scale;
            y *= scale;
            Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
            dir = normalize(dir);
            framebuffer[m++] = castRay(eye_pos, dir, scene, 0);
        }
        UpdateProgress(j / (float)scene.height);
    }

此时，生成的图片是有两个球体的：

第二，也就是通过Moller-Trumbore 算法来计算值，这个在课程有讲，所以直接套公式就行，其中算出来的t就是函数中的形参tnear，b1就是函数中的形参u，b2是函数中的形参v

  
bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig,
                          const Vector3f& dir, float& tnear, float& u, float& v)
{
    // TODO: Implement this function that tests whether the triangle
    // that's specified bt v0, v1 and v2 intersects with the ray (whose
    // origin is *orig* and direction is *dir*)
    // Also don't forget to update tnear, u and v.
    Vector3f e1 = v1 - v0;
    Vector3f e2 = v2 - v0;
    Vector3f s = orig - v0;
    Vector3f s1 = crossProduct(dir, e2);
    Vector3f s2 = crossProduct(s, e1);
    tnear = (1 / dotProduct(s1, e1)) * dotProduct(s2, e2);
    u = (1 / dotProduct(s1, e1)) * dotProduct(s1, s);
    v = (1 / dotProduct(s1, e1)) * dotProduct(s2, dir);

    if (u > 0 && v > 0 && u + v < 1 && tnear > 0)
    {
        return true;
    }
    return false;
}

在做的时候，我把更新tnear、u、v放在了检测出射线和三角形相交的代码块中，导致图片中地面的颜色是黑色的，实际上每次都应该更新，因为这个光线（也就是primary ray）没有打到三角形（也就是平面）的话，应该是有颜色的，如果不更新uv，就无法正常计算颜色了

GAMES101-Lecture 13 Ray Tracing 1(Whitted-Style Ray Tracing) & 作业5

Why Ray Tracing

Basic Ray-Tracing Algorithm

Light Rays(假设的条件)

Ray Casting

Recursive（Whitted-Style）Ray Tracing

Ray-Surface Intersection

Ray Equation

Ray Intersection With Sphere(Implicit Surface)

Ray Intersection With Triangle Mesh(emplicit Surface)

Moller Trumbore Algorithm

Accelerating Ray-Surface Intersection

Bouding Volumes(包围体积)

作业5

相关文章

GAMES101-Lecture 01 Overview of Computer Graphics

GAMES101-Lecture 02 Review of Linear Algebra

GAMES101-Lecture 03 Transformation