Surfaces
Subdivision,simplification,regularization
- 此处承接上一节课
- Mesh subdivision
- Mesh simplification
- Mesh regularization
Subdivision
Loop Subdivision
(因为发明这个算法的人叫loop,而不是循环的意思)
三角形数量增多
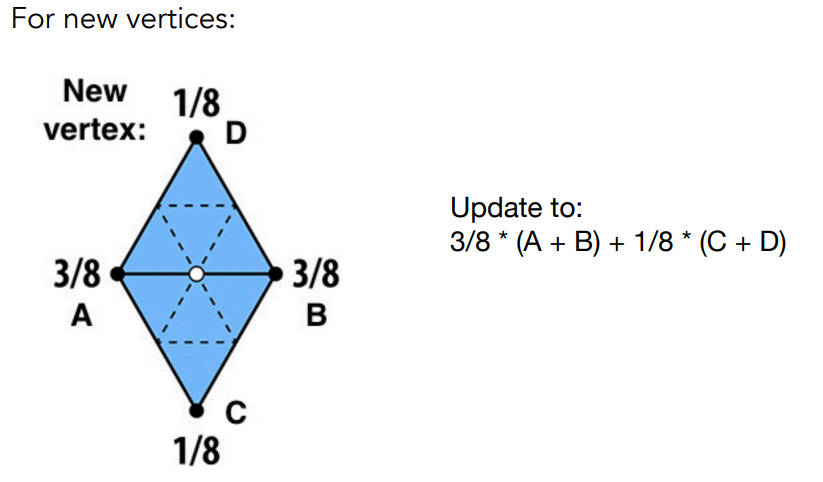
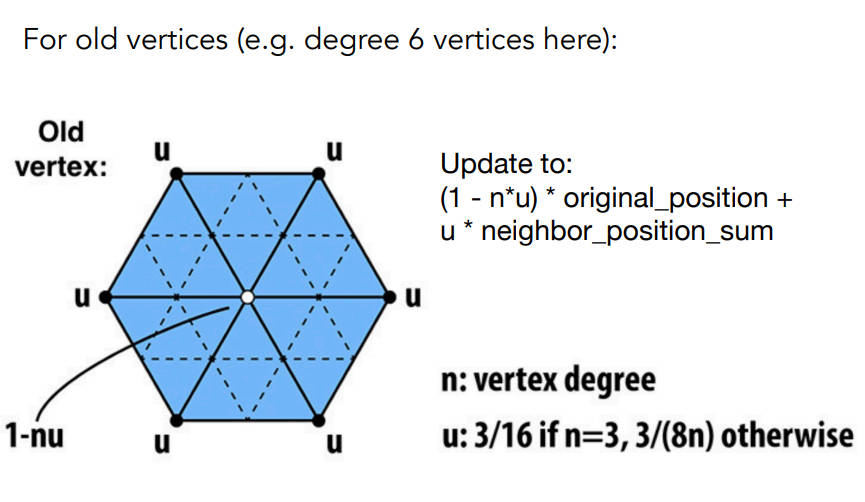
调整三角形顶点的位置,先区分新老顶点,然后使用不同的规则进行改变
对于新点,公式如下,以白色点为例子,根据贡献加权
对于老点,也是以下下面的图中的白色点为例子,算n(是一个点的度数即连接了几条边)和u,对于老点,不仅要考虑周围点的贡献还要考虑自身的贡献
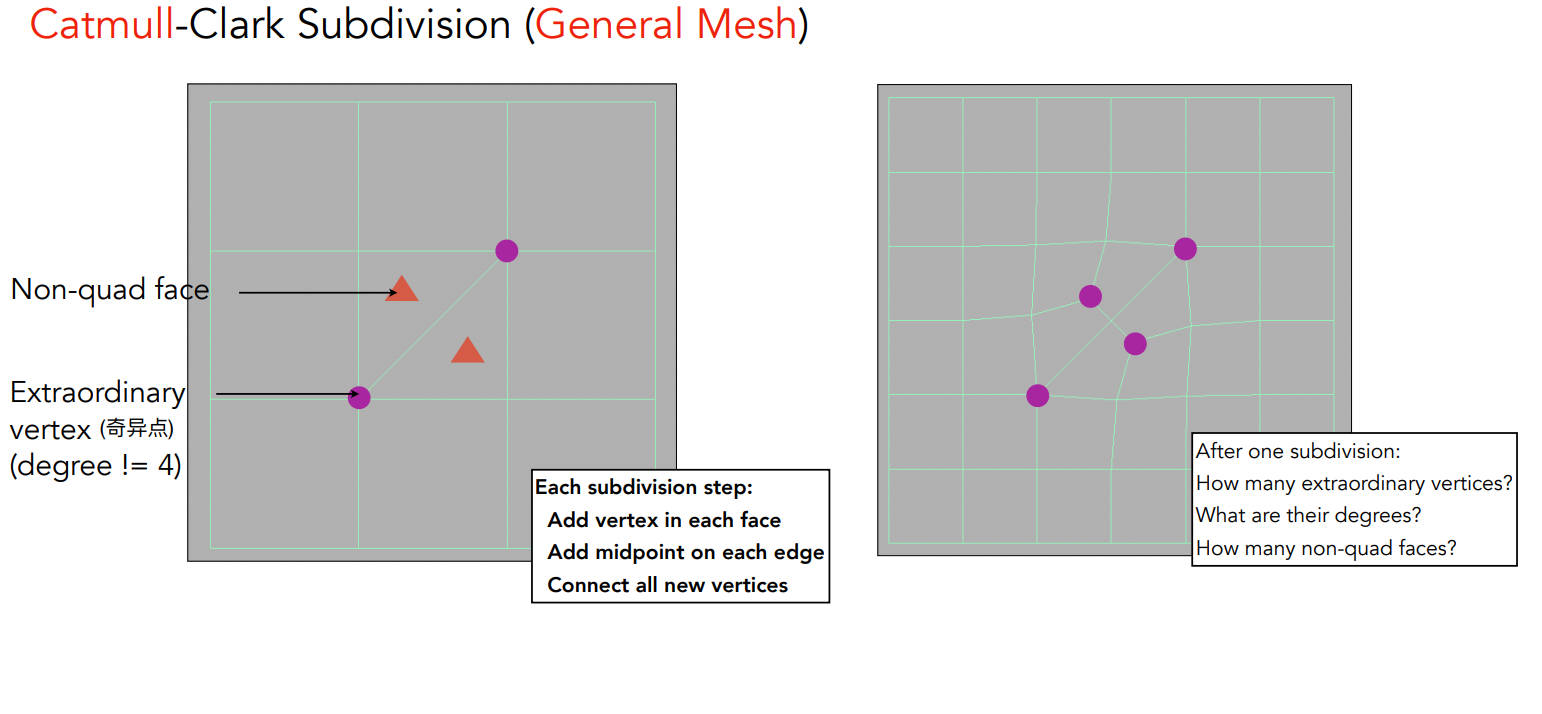
Catmull-Clark Subdivision
奇异点:度数不等于4的顶点
在Catmull-Clark细分一次后,所有的非四边形面都会变成一个奇异点,且不再有非四边形面
再多次细分后,也不会有新的奇异点了,因为一次细分后就不再有非四边形面了
- 点的更新方式分三种,新的面上的点,新的边上的点,老的点
- loop细分只能分三角形面,但Catmull-Clark细分可以细分四边形
Mesh Simplification
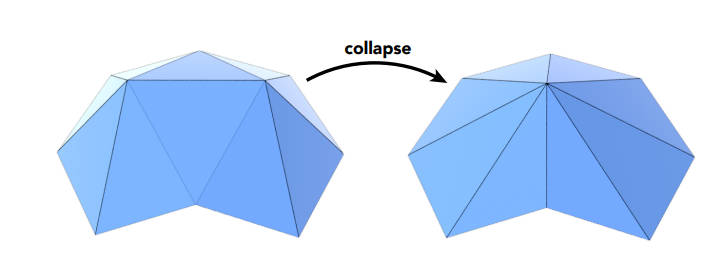
Edge collapsing 边坍缩
相当去删掉一条边变成一个点,那么问题就是删掉什么边
此时引入一个概念就是二次误差度量Error Metrics:新生成的点到与之关联的所有面的距离平方和的最小值,与之关联就是原来那条边的两点关联的所有面,下图中所有面都是相关联的
所以边坍缩就是去计算每条边的二次误差度量,排序,然后按顺序坍缩
但是会出现很多问题,首先是一条边坍缩后,相关联的很多边都会变化,所以需要一种数据结构,既能找到最小值又能动态修改每条边的二次误差度量值,也就是优先队列或者说是堆
Shadow Mapping
在做阴影计算的时候是不需要知道场景的几何信息的
会产生走样现象
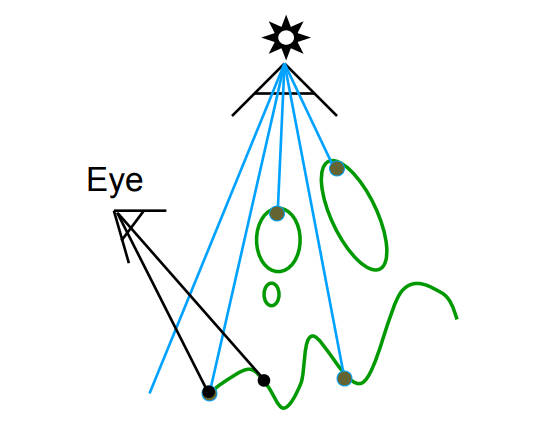
关键:非阴影点必须能够被光源(点光源)和摄像机看到
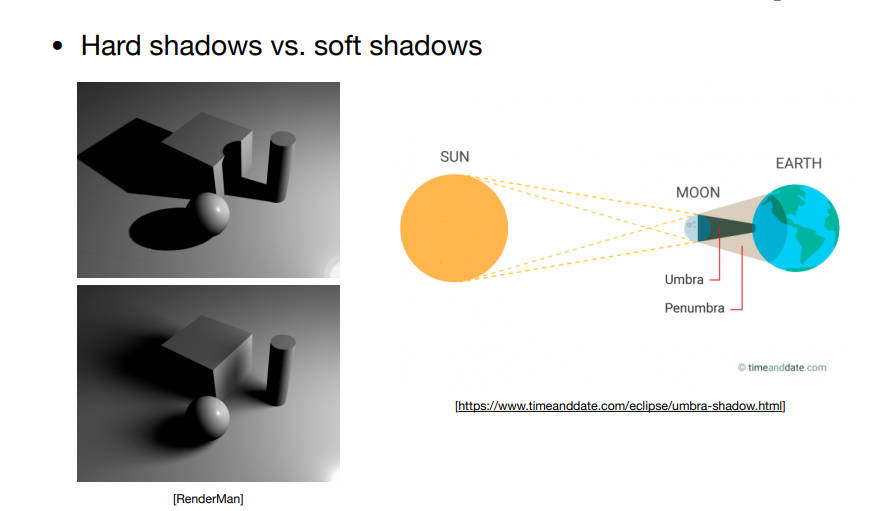
这种阴影也叫硬阴影
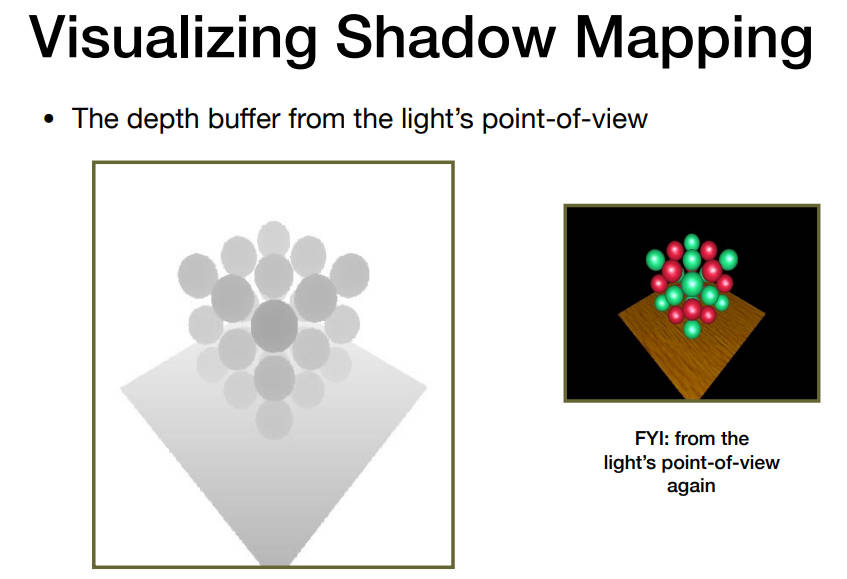
第一,储存光源能看到的点的深度值(其实这就生成了shadow map)
第二,从摄像机看到点,把该点投影到光源光栅化的那个平面的位置,去检测该位置储存的深度值(上一条储存的深度值)和该点本身的深度值(即该点到光源的距离)是否一致,如果一致,说明这个点,光源能看到,摄像机也能看到;如果不一致,说明,摄像机能看到,而光源看不到,那么这个点就是阴影点
- 但存在很多问题,第一,深度值是个浮点数,而浮点数的相等是很难的,所以就会出现下面这张图的问题(其中绿色是非阴影点,黑色和灰色是阴影点,颜色应该是光源视角平面上存的深度值),所以会设置一个很小的数值(scale、bias、tolerance),但是只能治标不治本
还有问题就是分辨率的问题,shadow map的分辨率和最后渲染的分辨率的问题就会产生走样(低分辨率、不同分辨率都会走样)
但是依旧是应用广泛的一种方法
软阴影就是因为有本影、半影的存在才会存在,如果有软阴影,那么说明光源有大小