GAMES101-Lecture 11 Geometry 2(Curves and Surface) & 作业4

Explicit Representations

• Point Cloud点云

  • 好表达

  • 大数据集很有用

  • 经常用于转换成多边形mesh

  • 难以在采样不足的区域进行绘制

• Polygon Mesh

  • 储存顶点和多边形

  • 方便处理、模拟、适合采样

  • 数据结构更复杂

  • 几乎最常见的显式表示

• wavefront object

  • v是顶点坐标

  • vt是纹理坐标

  • vn是法线

  • f是点的连接关系

Curves

Bezier curves

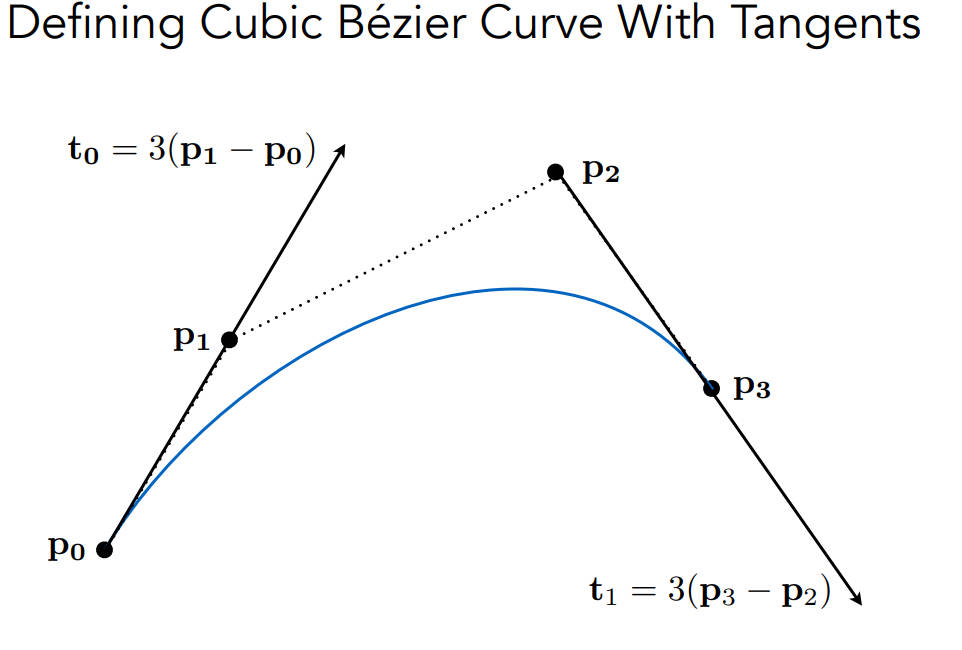
• 定义

  • 起始点在p0，终点在p1

  • 且起始点处的切线方向为p0p1，终点处的切线方向为p2p3

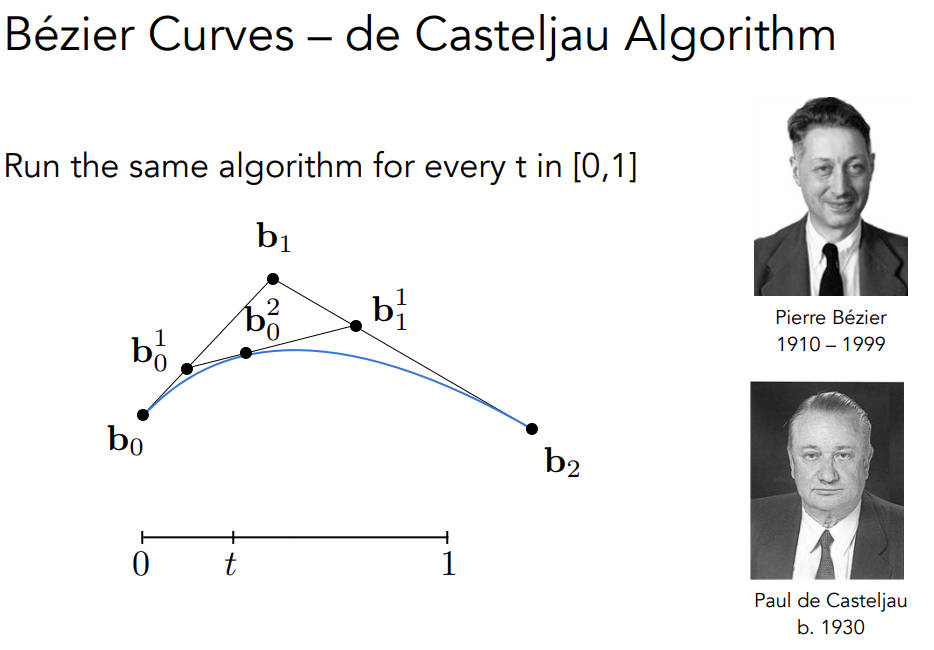
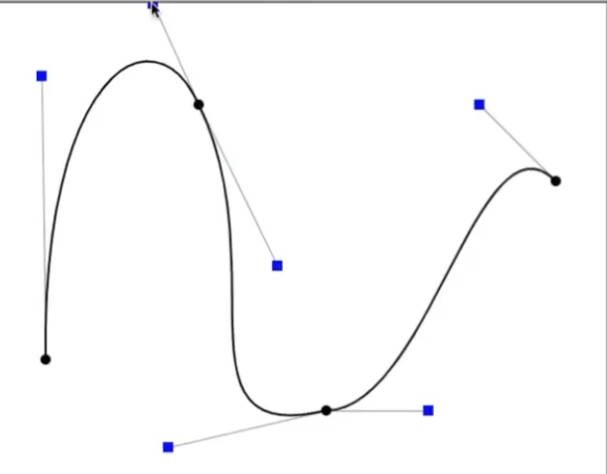
De Casteljau’s algorithm

• 这个算法需要至少三个控制点

  • 需要不断的取t[0,1]来采样，连接成一条曲线

  • 比如t = 1/3时，取b01点使得b0b01占b0b1的1/3，取b11点使得b1b11占b1b2的1/3，然后在b01b11取点b02使得b01b02占b01b11的1/3

  • 那么在t = 1/3时，曲线过点b02

  • 以此类推

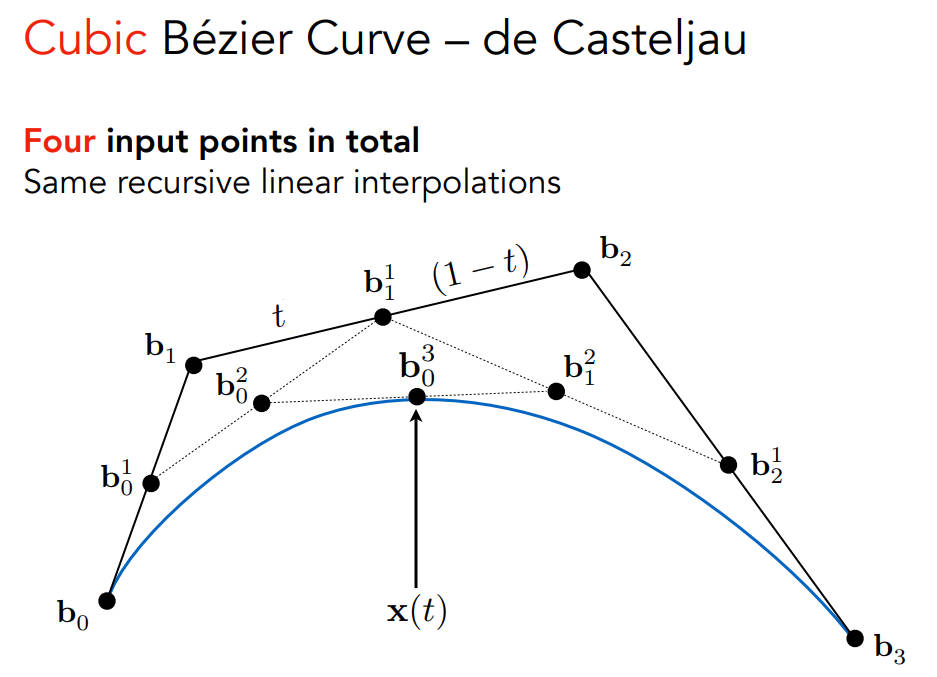
• 三次贝塞尔曲线，需要四个点，操作跟上面的类似

• 公式就是不断地插值，递归

• n是曲线的degree，如果有3个控制点，那n就是2，B是伯恩斯坦多项式

• 在三维空间中依然适用

• 贝塞尔曲线的性质：

  • 起始点和终点确定

  • 起始点和终点切线方向确定

  • 仿射变换的结果一样（对控制点先变换再画线和先画线再对线上的控制点变换），但对投影不一样

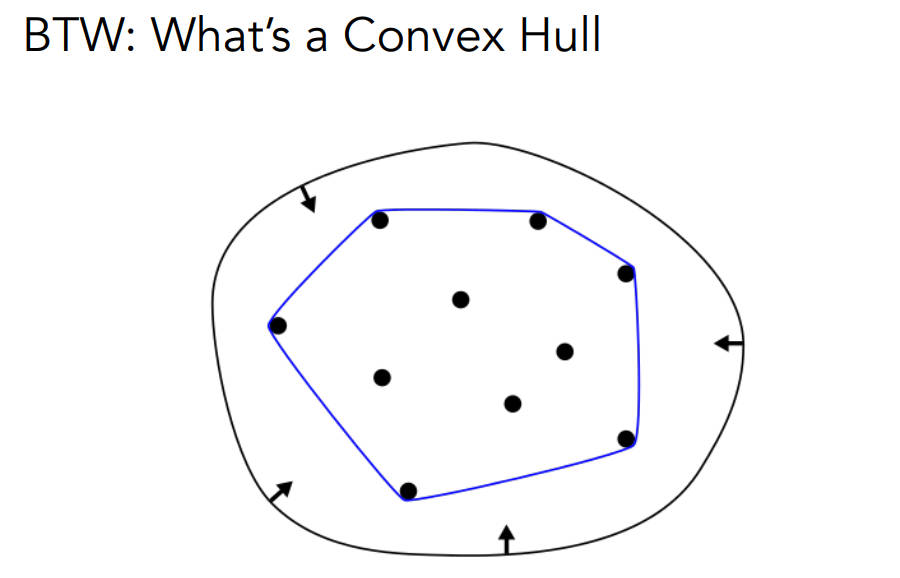
  • 凸包性质：曲线一定在控制点形成的凸包内

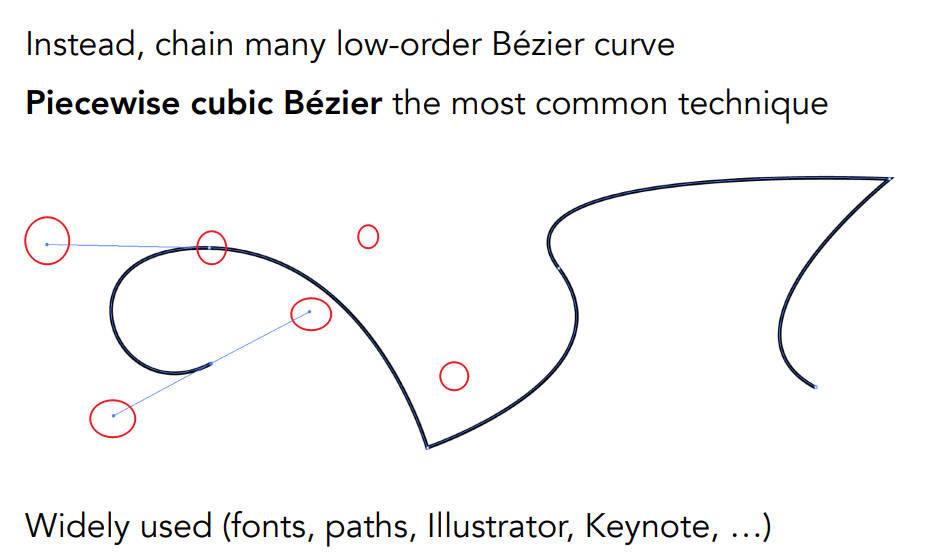
Piecewise Bezier Curves 多段贝塞尔

• 最常用的是三次贝塞尔曲线（4个控制点）

• 当一个终点控制点（连接两条曲线）相邻两个控制点在一条直线上且距离该终点距离相同，那么这两条曲线实现了平滑的连接

• 如果在一条直线上但距离该终点距离不相同，那么不算平滑连接。比如一个蚂蚁爬到终点时会突然加速

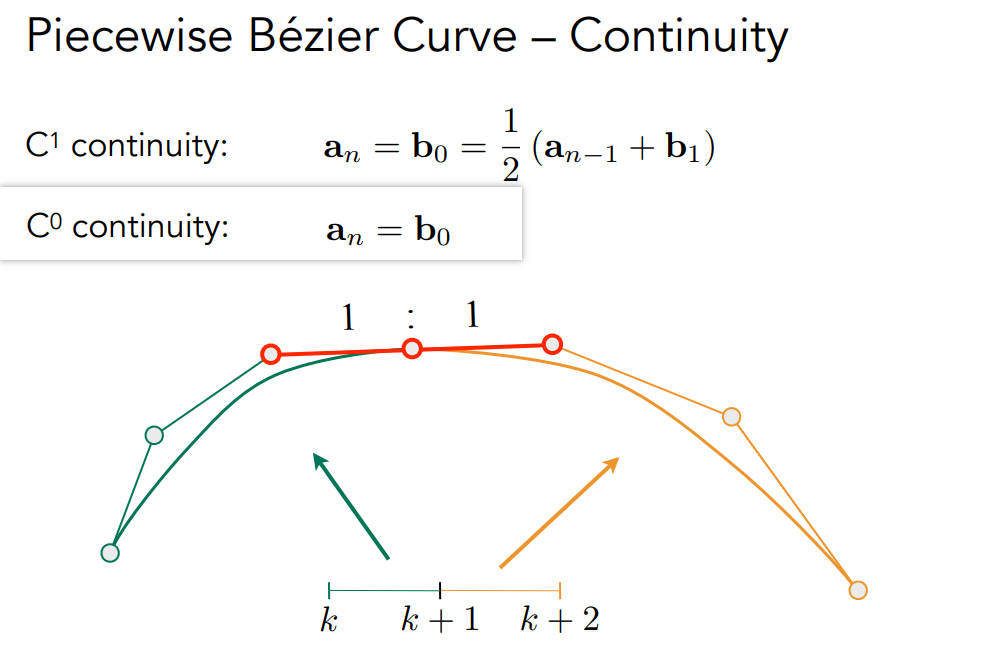
• C0连续：第一段的终点和第二段的终点重合

• C1连续：第一段的终点和第二段的终点重合，且第一段的an-1点和第二段的b1点在一条直线上，且距离重合点距离相等（相当于第一段的终点和第二段的终点的一阶导数相等）

• C2连续：C1的基础上，二阶导数再相等

B-splines（basis splines）

• B样条不需要分段就具有局部操控性（动一个点不会整条曲线都改变）

• 极其复杂

• 非均匀有理B样条（NURBS）更复杂

Surfaces

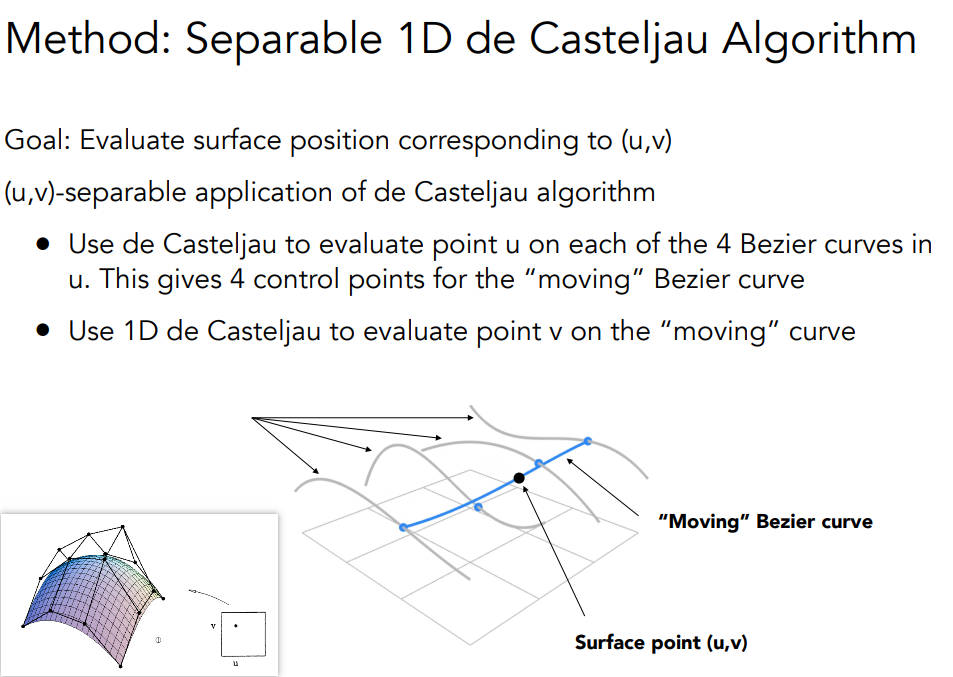
Bezier surfaces

• 首先，现在有16个点，每行4个，先根据每行的4个点画出四条曲线，然后根据t，在四条线上一共会找到四个点，再根据这四个点来绘制列的曲线

• uv上的任何一个点都可以映射到曲面上，uv可以理解成t1和t2

• 所以贝塞尔曲线是显式表示，因为它可以被映射而来

Subdivision,simplification,regularization

作业4

• 作业描述：

• Bézier 曲线是一种用于计算机图形学的参数曲线。在本次作业中，你需要实

  现 de Casteljau 算法来绘制由 4 个控制点表示的 Bézier 曲线 (当你正确实现该

  算法时，你可以支持绘制由更多点来控制的 Bézier 曲线)。

  你需要修改的函数在提供的 main.cpp 文件中。

  • bezier：该函数实现绘制 Bézier 曲线的功能。它使用一个控制点序列和一个OpenCV：：Mat 对象作为输入，没有返回值。它会使 t 在 0 到 1 的范围内进行迭代，并在每次迭代中使 t 增加一个微小值。对于每个需要计算的 t，将调用另一个函数 recursive_bezier，然后该函数将返回在 Bézier 曲线上 t处的点。最后，将返回的点绘制在 OpenCV ：：Mat 对象上。

  • recursive_bezier：该函数使用一个控制点序列和一个浮点数 t 作为输入，实现 de Casteljau 算法来返回 Bézier 曲线上对应点的坐标。

• 这次的作业非常简单，就是平滑得写一小会儿

• 递归就是按ppt的思路递归，没啥好说的

• cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t) 
  {
      // TODO: Implement de Casteljau's algorithm
      if (control_points.size() == 1)
      {
          return control_points[0];
      }
      std::vector<cv::Point2f> new_points;
      for (int i = 0; i < control_points.size()-1; i++)
      {
          float x = t * control_points[i].x + (1 - t) * control_points[i + 1].x;
          float y = t * control_points[i].y + (1 - t) * control_points[i + 1].y;
    
          new_points.emplace_back(x,y);
      }
      return recursive_bezier(new_points, t);
  }
  

• 然后仿照naive_bezier函数画点即可

• void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
  {
      // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
      // recursive Bezier algorithm.
      for (float t = 0.0; t <= 1.0; t += 0.001)
      {
          auto point = recursive_bezier(control_points, t);
          window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
          }
    
      }
  }
  

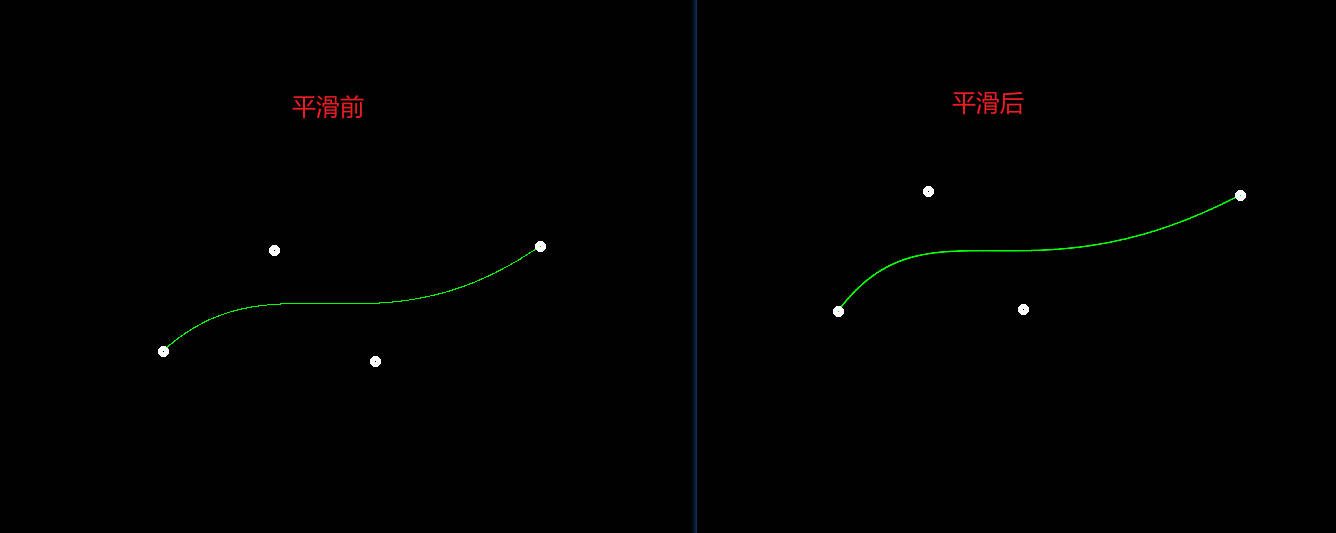
• 平滑的话，就是先跟上次作业中的双线性插值一样，判断要平滑的是哪四块像素，然后计算点到四个像素中心的距离d1、d2、d3、d4，根据比例来赋颜色值

• void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
  {
      // TODO: Iterate through all t = 0 to t = 1 with small steps, and call de Casteljau's 
      // recursive Bezier algorithm.
      for (float t = 0.0; t <= 1.0; t += 0.001)
      {
          auto point = recursive_bezier(control_points, t);
          window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
          bool smooth = false;
          if (smooth)
          {
              float d1, d2, d3, d4;
              int x = point.x;
              int y = point.y;
              d1 = dis(point.x, point.y, (float)x + 0.5f, (float)y + 0.5f);
              int xx, yy;
              if (point.x - (float)x - 0.5f > 0.f)
              {
                  xx = x + 1;
              }
              else
              {
                  xx = x - 1;
              }
              d2 = dis(point.x, point.y, (float)xx + 0.5f, (float)y + 0.5f);
              setColor(xx, y, 255.f * d1 / d2, window);
              if (point.y - (float)y - 0.5f > 0.f)
              {
                  yy = y + 1;
              }
              else yy = y - 1;
              d3 = dis(point.x, point.y, (float)x + 0.5f, (float)yy + 0.5f);
              setColor(x, yy, 255.f * d1 / d3, window);
              d4 = dis(point.x, point.y, (float)xx + 0.5f, (float)yy + 0.5f);
              setColor(x, yy, 255.f * d1 / d4, window);
          }
    
      }
  }
  

• 其中，为了方便创建了两个函数

• float dis(float x1, float y1, float x2, float y2)
  {
      return sqrt( pow(x2 - x1, 2) + pow(y2 - y1, 2));
  }
  void setColor(int x, int y, float c, cv::Mat& window)
  {
      if (x < 0) x = 0;
      if (x > window.cols) x = window.cols - 1;
      if (y < 0) y = 0;
      if (y > window.rows) y = window.rows - 1;
      window.at<cv::Vec3b>(y, x)[1] = std::max(c, (float)window.at<cv::Vec3b>(y, x)[1]);
  }