Blinn-Phong(后半部分)
Specular Term(Blinn-Phong)
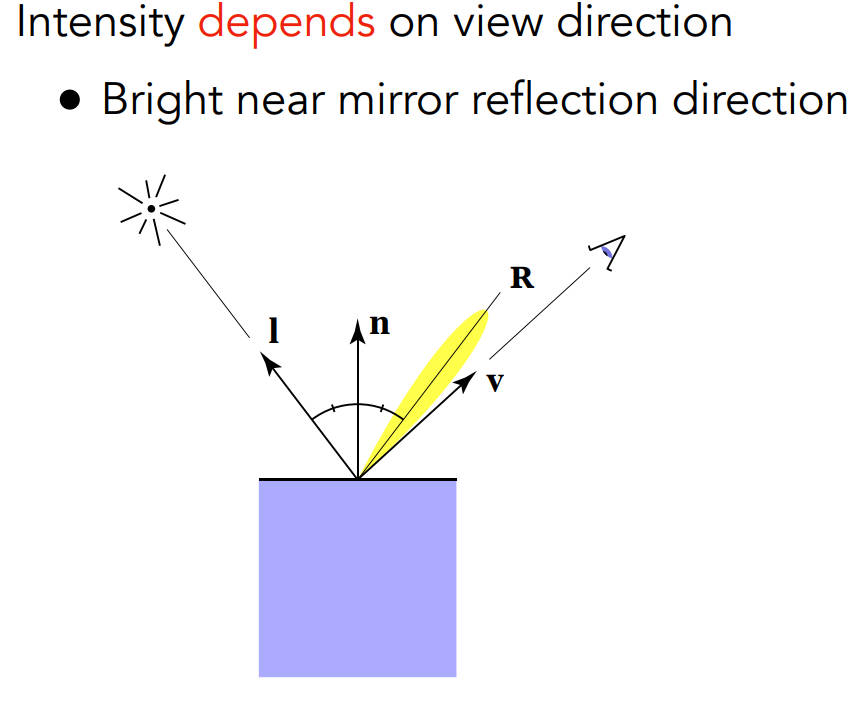
观察方向和镜面反射方向接近时,就能看到高光项
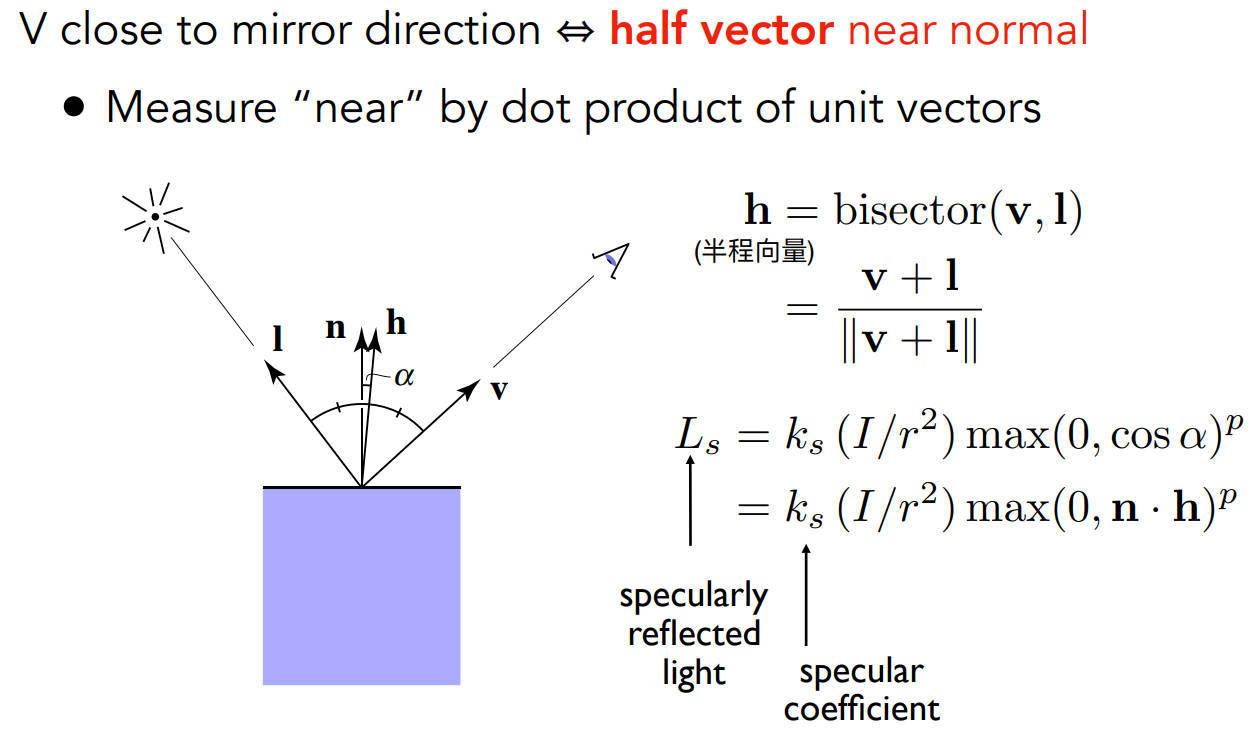
注视方向加光照方向(平行四边形法则)就能得到半程向量的方向,如果h和n(法线方向)接近,就说明和镜面反射方向很接近,就能看到高光
- \[\pmb{h}(半程向量)=bisector(\pmb{v},\pmb{l}) \\ =\frac{\pmb{v}+\pmb{l}} {\lVert \pmb{v}+\pmb{l}\rVert}\]
Ls时镜面反射光强度,Ks时镜面系数,其实就是一个颜色(三通道),通常是白色
- \[L_s = k_s(I/r^2)max(0,cos\alpha)^p \\ =k_s(I/r^2)max(0,\pmb{n\cdot h})^p\]
直接算R(镜面反射方向)和V向量的点乘是Phong反射模型,半程向量和法向量做点乘叫Blinn-Phong,这是个改进,因为半程向量相对于反射方向向量来说更好算
- 这里不考虑吸收和不吸收的颜色是因为phong是个经验模型,简化了这一点
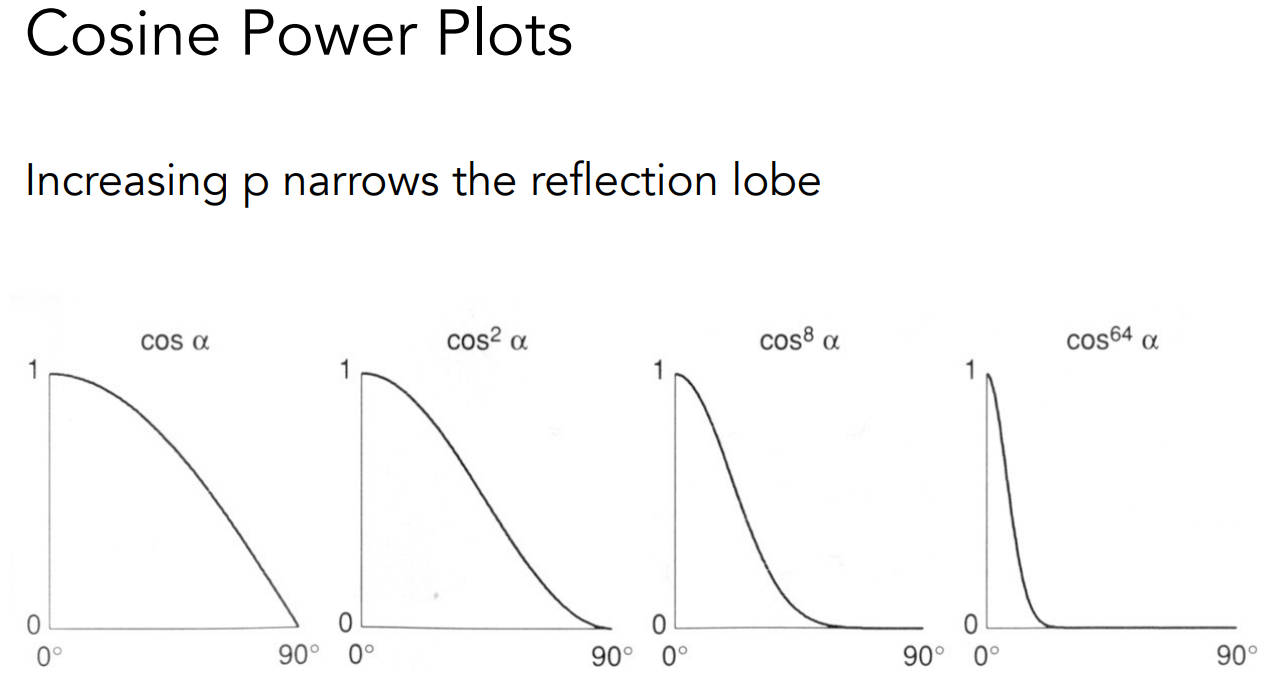
- 加个p的指数是为了降低余弦的“容忍度”,p越大,那么度数增加一点就会让$max(0,\pmb{n\cdot h})^p$值下降很多,意味着,偏很小的角度就看不到高光了,p通常取100到200。相同物体,同一方向去看的话,随着p增大,高光范围会逐渐缩小成一个点
Ambient Term
假设来自四面八方的环境光照强度一样,那么环境光照强度就是一个常数(实际上不是这样),$k_a$是环境光系数,其实就是颜色,$I_a$是环境光照的强度
- \[L_a = k_aI_a\]
Blinn-Phong Reflection Model
Ambient+Diffuse+Specular=Blinn-Phong Reflection
- \[L = L_a+L_d+L_s \\ =k_aI_a+ k_d(I/r^2)max(0,\pmb{n\cdot l}) +k_s(I/r^2)max(0,\pmb{n\cdot h})^p\]
Shading Frequencies(着色频率)
要把着色应用在哪些点上
Shade each triangle(flat shading)
计算每个三角形的法线,三角形的两边做一个叉乘
Shade ezch vertex(Gouraud shading)
求每个顶点的法线方向,根据每个顶点的颜色,通过插值来计算顶点内部颜色的大小
三角形顶点的法线可以通过两种主要方法计算:
面法线计算法:首先计算三角形面法向量,再使用向量插值法求出三个顶点的法向量。面法向量可以通过三角形两边向量的叉积求得。此方法的优点是顶点法线与面法线垂直,缺点是不够平滑,会出现明显的法线变化。
法线平滑法:考虑三角形每个顶点附近的所有相邻三角形,使用所有相邻三角形的面法向量计算顶点法线。通过叠加相邻面法向量再归一化得到平滑的顶点法线。此方法可以产生更平滑的法线变化,但法线不再垂直于面。一般来说,法线平滑法可以产生更高质量的渲染结果,所以更为广泛使用。其计算步骤如下:
找出每个顶点p附近的所有相邻三角形。
计算每个相邻三角形的面法线ni。
求出这些面法线的叠加和:n = n1 + n2 + … + nn
对叠加的法线和进行归一化,得到顶点p的平滑法线:np = normalize(n)
利用顶点的平滑法线np和光照参数计算顶点颜色。
使用Gouraud着色,根据三角形每个顶点颜色为三角形内部所有像素点着色。所以,三角形顶点的法线主要通过两种方法计算:
面法线计算法:简单但不够平滑。
法线平滑法:考虑相邻面信息,可以产生平滑的法线,这也是更为常用的方法。平滑的顶点法线为之后的光照计算和Gouraud着色提供信息,能渲染出更高质量的三维图像。
Shade each pixel(Phong shading)(这是一种着色频率)
根据三角形三个顶点的法线,插值求出三角形内部每个像素的法线方向,对每个像素进行着色,根据像素点法线向量和光照参数计算该点的漫反射光强、镜面高光强度等。
flat着色和Gouraud着色区别是:flat每个面一个法线,而Gouraud每个顶点一个法线,也就是每个三角面三个法线,因此计算出来的三个顶点的颜色是不同的,后面插值后,三角面内部的颜色也就是根据这三个顶点插值的
Gouraud着色,Phong着色的区别是:Gouraud直接根据插值计算像素的颜色值,Phong根据插值计算每个像素的法线,然后根据法线再算每个像素的颜色
相比Gouraud着色,Phong着色的主要优势在于:
Phong着色在每个像素点都确定一种颜色,而Gouraud着色在三角形内部进行插值。所以Phong着色没有Gouraud着色的马素尔效应,渲染更为平滑。
Phong着色直接使用每个像素点的法线进行光照计算,可以很好的渲染出镜面高光等效果。而Gouraud着色只使用三角形顶点法线,高光效果较差。
Phong着色考虑每个像素点的明确光照,可以产生更真实的阴影效果。Gouraud着色通过色彩插值很难实现精确的阴影。
当面出现的频率较高时,使用平滑着色也可以。
- 当面数超过像素数,Phong着色开销自然也会比平滑着色小了
Defining Per-vertex Normal Vectors
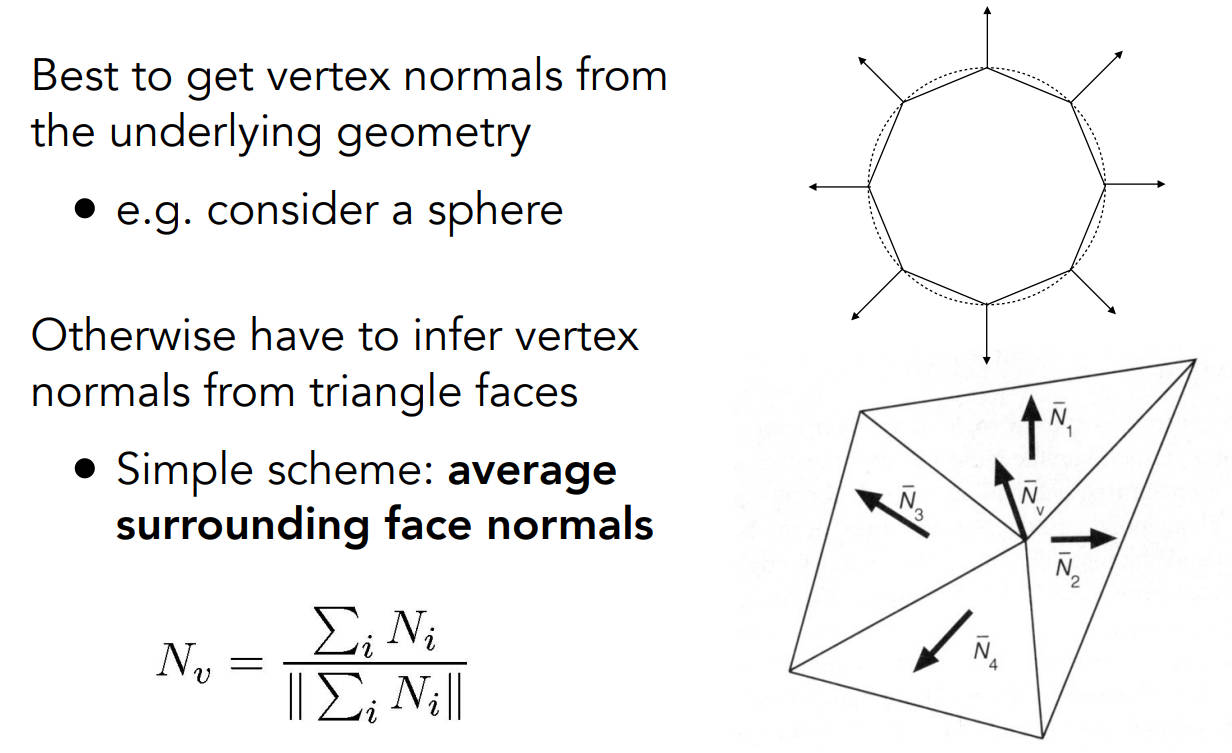
1.考虑是一个球,直接圆心到顶点
2.顶点相邻面的法线求个平均(根据三角形面积加权)
\[N_v = \frac{\sum_iN_i}{\lVert \sum_iN_i \rVert}\]
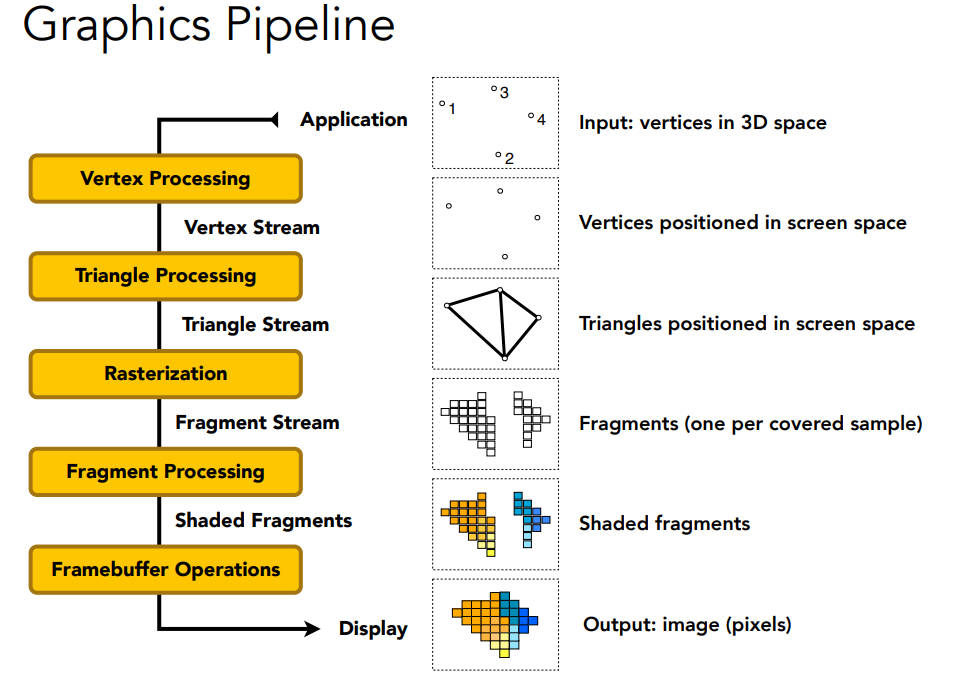
Graphics(Real-time Rendering)Pipline
application:Input vertices in 3D space
Vertex Processing(Vertex Stream): Vertices positioned in screen space
Trangle Processing(Triangle Stream):Trangles positioned in screen space
Rasterization(Fragment Stream):Fragments(one per covered sample)一个fragment就是一个像素
Fragment Processing(Shaded Fragments):Shaded Fragments
Frambuffer Operations
Display:Output image(pixels)
mvp变换在Vertex Processing阶段
对每个像素采样,在Rasterization阶段
判定可见性(z-buffer)在Fragment Processing阶段
如果是顶点着色,那么在Vertex Processing阶段,如果是Phong着色,在Fragment Processing阶段
Shader Programs
shader程序应用于每一个顶点或像素(不用写for循环)
着色器有两种,顶点着色器和像素/片段着色器
像素着色器:算像素最后的颜色
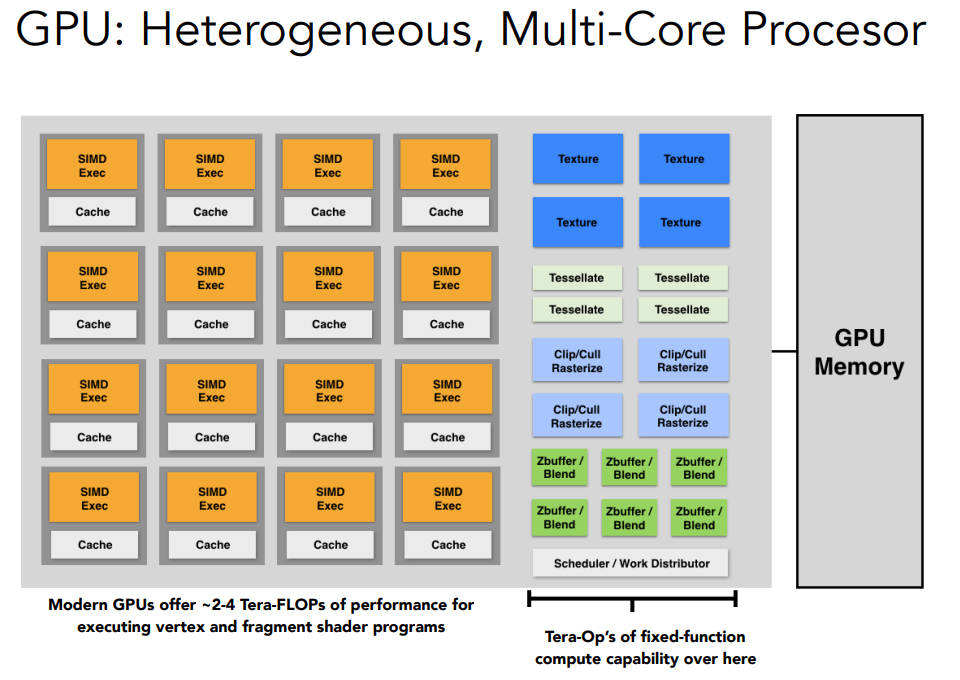
GPU
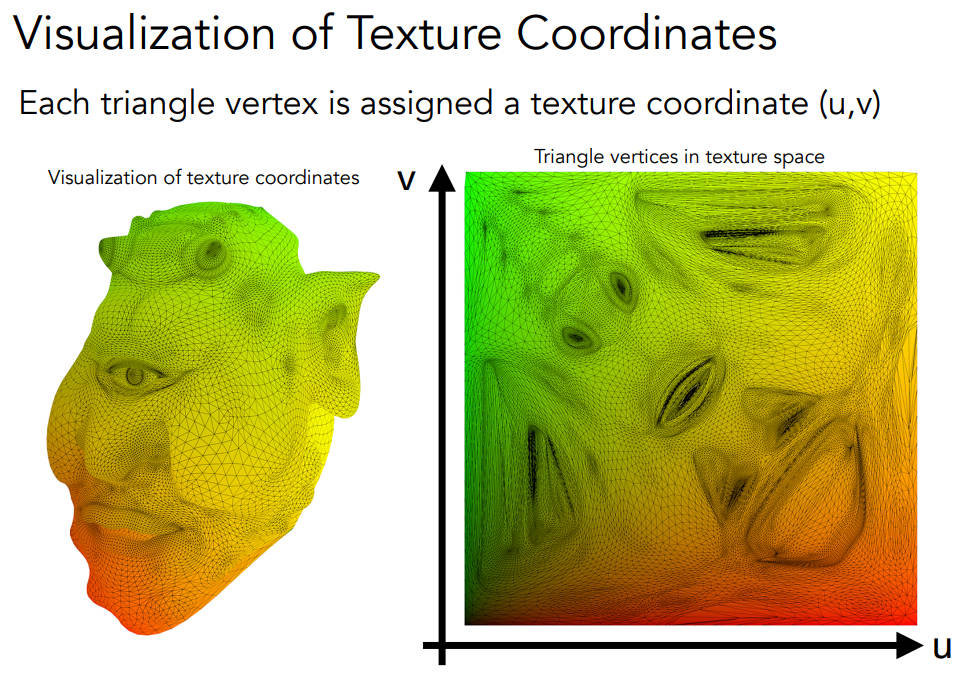
Texture Mapping
- 任何三维物体的表面都是二维的
- UV图(纹理图),u和v的范围都在[0,1]
三角形每个顶点都对应着一个uv
tiled textures(无缝衔接的纹理)