GAMES101-Lecture 05 Rasterization 1 (Triangles) & 作业1

Transformation

这一节其实是沿着上一节的viewing讲剩下的一小部分，然后开了个光栅化的头

Perspective Projection

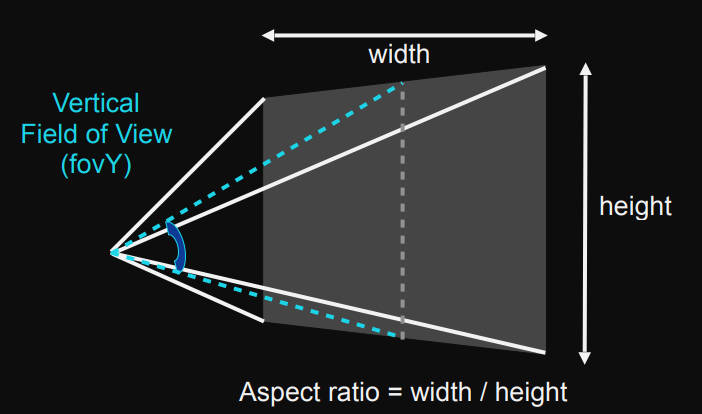
aspect ratio = width/height宽高比(r就是right，t就是top)
\[aspect=\frac{r}{t}\]
field-of-view(fovY)垂直可视角度(t就是top，n就是near，因为朝-z方向，所以取个绝对值)
\[\tan\frac{fovY}{2} = \frac{t}{\lvert n \rvert}\]
mvp变换

Canonical Cube to Screen

屏幕
- 像素的二维数组
- 数组的大小就是分辨率
- 典型的光栅显示

变换xy平面：$[-1,1]^2到[0,width]\times[0,height]$
视口变换：先缩放（因为l到r是-1到1，所以缩放需要缩成$(-\frac{width}{2},\frac{width}{2})$），再把中心从原点移到$(\frac{width}{2},\frac{height}{2})$，这样，原点就在左下角了
\[M_{viewport}= \left( \begin{matrix} \frac{width}{2} & 0 & 0 & \frac{width}{2}\\ 0 & \frac{height}{2} & 0 & \frac{height}{2}\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right)\]

Frame Buffer: Memory for a Raster Display

图像会存在显存中的不同区域中，告诉显示器显示哪一副图

LCD(Liquid Crystal Display) Pixel(液晶显示)

LED Array Display 发光二极管

Triangles-Fundamental Shape Primitives

三角形：
- 最基础的多边形
- 其他多边形可以拆成三角形
- 独特的性质：
  - 一定是平面
  - 三角形内外定义清晰
  - 便于渐变

Sampling

判断像素的中心是否在三角形内

  
for(int x = 0; x < xmax; ++x)
    for(int y = 0; y < ymax; ++y)
        image[x][y] = inside(tri, x+0.5, y+0.5);

已知Q点和三角形$P_0P_1P_2$，分成三个向量：$\vec{P_0P_1}$、$\vec{P_1P_2}$、$\vec{P_2P_0}$，分别和$\vec{P_0Q}$、$\vec{P_1Q}$、$\vec{P_2Q}$做叉积，如果得到的向量方向一致，说明点Q在三条边的同侧（如都在边的左侧），那么就在三角形内，否则（一旦出现叉积结果方向不一致），就说明在三角形外。
边界情况：要么不做处理，要么特殊处理。
使用包围盒检测三角形附近的点，也就是三个点x的最大最小，y的最大最小
使用每一行的最小最大值进行检测，适合细长且倾斜的三角形
Aliasing走样：Jaggies锯齿

作业1

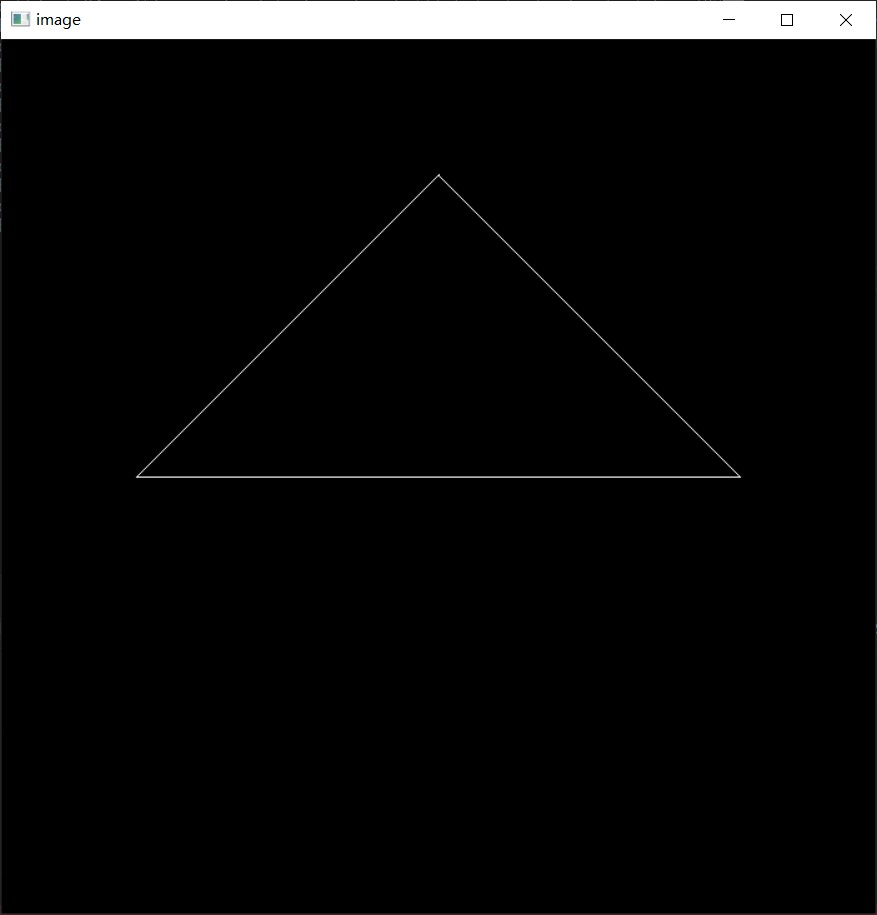
任务描述：本次作业的任务是填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个
点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0), 你需要将这三个点的坐
标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形 (在代码框架中，我们已
经提供了 draw_triangle 函数，所以你只需要去构建变换矩阵即可)。
环境构建，其实就是添加Eigen库和Opencv的库
- 配置库查看这个博客：手把手教你games101环境搭建（图文并茂）——Visual Studio安装，Eigen库，Opencv配置_亭墨的博客-CSDN博客
- 还有就是为了避免每次做新的作业就要配一遍库，创建一个项目属性表：(vs2019+opencv环境配置，不用每次都设置属性目录_vs 每次都要配置包含目录_小明今天学习了吗的博客-CSDN博客
其实不难，就是写下模型矩阵（旋转矩阵）和透视投影矩阵，但我遇到了很多很多问题，最后不得已去搜索了，查出很多错，实在惭愧，先贴代码吧，之后写下注意事项

get_model_matrix函数：

这个函数其实就是绕Z轴旋转的矩阵，需要注意的是cos里面的参数是弧度值，要把度数转换成弧度值才行

  
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
  
    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    Eigen::Matrix4f translate;
    translate << std::cos(rotation_angle / 180.0 * MY_PI), -std::sin(rotation_angle / 180.0 * MY_PI), 0.0, 0.0,
        std::sin(rotation_angle / 180.0 * MY_PI), std::cos(rotation_angle / 180.0 * MY_PI), 0.0, 0.0,
        0.0, 0.0, 1.0, 0.0,
        0.0, 0.0, 0.0, 1.0;
    model = translate * model;
    return model;
}

get_projection_matrix函数：
我在写这个函数的时候，漏洞百出。
- 首先，最最要命的错误就是矩阵公式不对，我记的笔记中，M1矩阵和M2矩阵的1记错位置了，这种问题真要我自己找根本找不到，这种错误太致命了。
- 其次是哪里出错呢，就是一些小地方，注释也都提到了，数行和列数错了，这种错误让我梦回中学时代。
- 还有就是，明明前面算cos的时候还记得弧度值，到后面算tan的时候就忘了。

  
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
    float zNear, float zFar)
{
    // Students will implement this function

    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.
    Eigen::Matrix4f orthographicM1 = Eigen::Matrix4f::Zero();
    Eigen::Matrix4f orthographicM2 = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f orthographic;
    Eigen::Matrix4f persp2ortho = Eigen::Matrix4f::Zero();
    float t = std::abs(zNear) * tan(eye_fov / 2 / 180 * MY_PI);//没有转换成弧度值
    float r = aspect_ratio * t;
    //M1:
    orthographicM1(0, 0) = 1 / r; //2 / r - l;
    orthographicM1(1, 1) = 1 / t;
    orthographicM1(2, 2) = 2 / std::abs(zNear - zFar);//一开始写成了1/...
    orthographicM1(3, 3) = 1.0;//这里一开始写成了3，2

    //M2:
    //orthographicM2.topLeftCorner(3, 3).setIdentity();//这里一开始写成了setZero
    //orthographicM2(3, 3) = 1.0;//这里一开始写成了3，2
    orthographicM2(2, 3) = -(zNear + zFar) / 2;//一开始写成了0，3
    //persp2ortho:
    persp2ortho(0, 0) = zNear;
    persp2ortho(1, 1) = zNear;
    persp2ortho(3, 2) = 1.0;//一开始写成了2，3
    persp2ortho(2, 2) = zNear + zFar;
    persp2ortho(2, 3) = -zNear * zFar;

    orthographic = orthographicM1 * orthographicM2;
    projection = orthographic * persp2ortho;

    return projection;
}

结果：

有一个问题就是，在main函数中r.set_projection(get_projection_matrix(45, 1, -0.1, -50));，函数传入的zNear和zFar要改成-的，不然会显示反着。
有个问题我还是不太懂，就是view矩阵，他其实就是做了个平移，相当于是z减少了5。问题就是相机的初始位置到底在哪里呢？很奇怪，是（0,0）吗，相机的注视方向呢？是沿着Z轴吗？相机的头顶方向呢？其实只要矩阵写对了，就能看到三角形，也许这道作业就是为了让我们了解下model变换和透视投影变换吧，其他的问题可能会在后面解决吧。

作业1重做版

20023.5.14
先说总结，这次跟上次有相似的地方也有不同的地方，但总的来说比上次更加理解了，没想到时隔数月还是又回来学games101了
其实代码大差不差，上代码。model矩阵就是用来旋转模型，其实就是控制三角形旋转的矩阵啦，记得要将度数转成弧度，这边记得，下边的tan又又又忘了转换，不过问题不大，没转的话只是相当于eye_fov数字变大了，三角形看起来变小了一点

  
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
  
    model(0, 0) = cos(rotation_angle/180.f* MY_PI);
    model(0, 1) = -sin(rotation_angle / 180.f * MY_PI);
    model(1, 0) = sin(rotation_angle / 180.f * MY_PI);
    model(1, 1) = cos(rotation_angle / 180.f * MY_PI);
  
    return model;
}

  
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    //aspect_ratio = r / t;
    //tan(eye_fov)/2 = t/|n|;
    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
    float t = tan(eye_fov / 2 /180.f *MY_PI) * abs(zNear);
    float b = -t;
    float r = aspect_ratio * t;
    float l = -r;
    Eigen::Matrix4f m1 = Eigen::Matrix4f::Identity();//缩放矩阵
    Eigen::Matrix4f m2 = Eigen::Matrix4f::Identity();//平移矩阵
    m1(0, 0) = 2.f / (r - l);
    m1(1, 1) = 2.f / (t - b);
    m1(2, 2) = 2.f / (zNear - zFar);
  
    m2(0, 3) = -(r + l) / 2.f;
    m2(1, 3) = -(t + b) / 2.f;
    m2(2, 3) = -(zNear + zFar) / 2.f;
  
    Eigen::Matrix4f Mortho = m1 * m2;//正交矩阵
  
    //平截头体压缩至长方体矩阵
    Eigen::Matrix4f Mpersp2ortho;
    Mpersp2ortho << zNear, 0.f, 0.f, 0.f,
        0.f, zNear, 0.f, 0.f,
        0.f, 0.f, zNear + zFar, -zNear * zFar,
        0.f, 0.f, 1.f, 0.f;
  
    projection = Mortho * Mpersp2ortho;
  
    return projection;
}

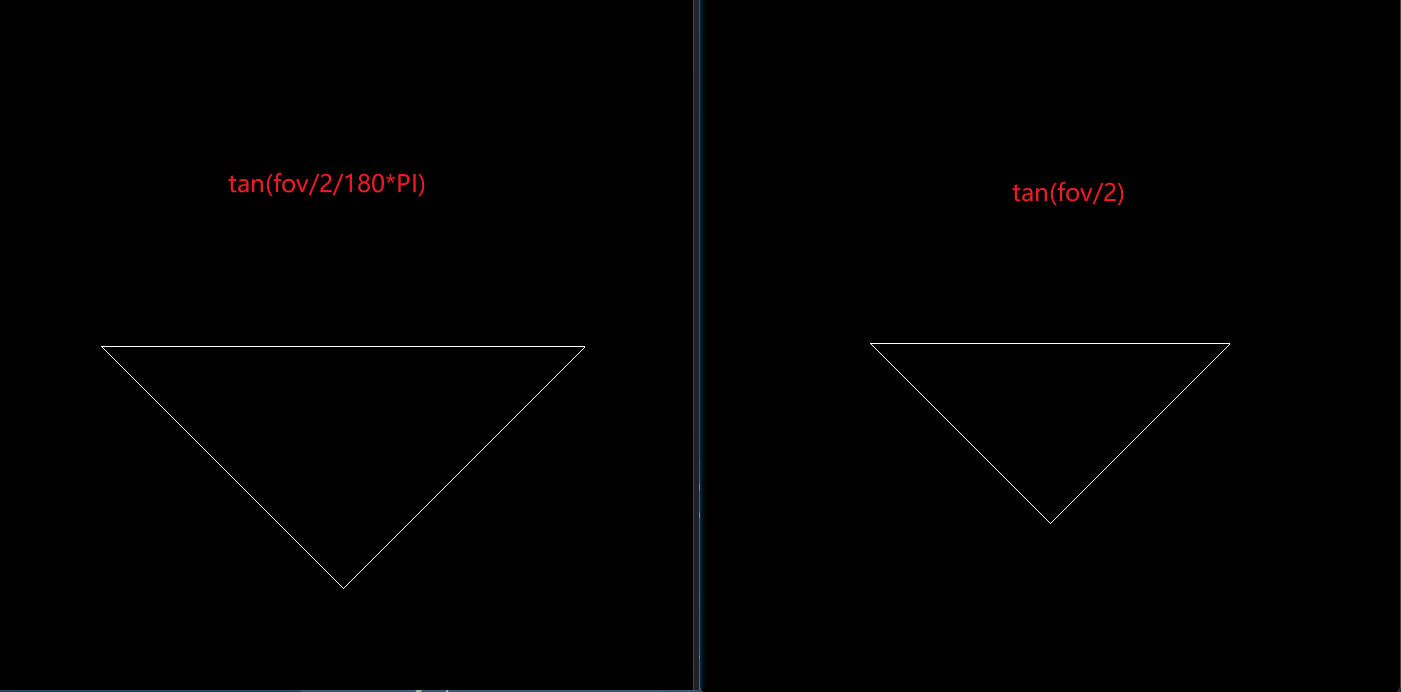
下面放两种tan的对比图

在main中设置zNear和zFar是正数（r.set_projection(get_projection_matrix(45, 1, 0.1, 50));），所以是倒三角，因为在projection矩阵中的m1矩阵（缩放矩阵）的第三行第三列也就是m1(2, 2)，因为zNear和zFar是正数且前者更小，所以总的结果是负数也就是说缩放的时候直接翻转了，只要把main函数中的设置投影矩阵函数的参数改为负数即可：r.set_projection(get_projection_matrix(45, 1, -0.1, -50));
- 详细说一下反转，在看了《GAMES101》作业框架问题详解 - 知乎 (zhihu.com)这篇博客后我有了点自己的理解，为什么z轴反转了三角形就倒过来了，我猜测是z轴翻转后，为了遵循坐标系的原则，导致x和y轴也转了一下。
- 如果三角形落在了摄像机后面也相当于z轴翻转了一下，跟上面一样
- 总之这个东西怪怪的，我觉得不用再深究了，后面遇到问题再处理，我认为我的猜想目前来看还是站得住脚的
接下来是提高部分，直接套课上讲的Rodrigues’ Rotation Formula公式即可，需要注意的是矩阵是4*4的，因为需要齐次坐标，代码如下：

  
Eigen::Matrix4f get_rotation(Eigen::Vector4f axis, float angle)
{
    Eigen::Matrix4f RotationMatrix;
    Eigen::Matrix4f IdentityMarix = Eigen::Matrix4f::Identity();
    Eigen::Matrix4f ProductMatrix;
    ProductMatrix << 0.f, -axis[2], axis[1], 0.f,
        axis[2], 0.f, -axis[0], 0.f,
        -axis[1], axis[0], 0.f, 0.f,
        0.f, 0.f, 0.f, 1.f;
  
    RotationMatrix = cos(angle / 180 * MY_PI) * IdentityMarix + (1 - cos(angle / 180 * MY_PI)) * axis * axis.transpose() + sin(angle / 180 * MY_PI) * ProductMatrix;
    return RotationMatrix;
}

那么如何调用呢？首先在main函数开头声明旋转轴和角度：

  
    float angle2 = 0;
    Eigen::Vector4f RotationAxis(1.f,0.f,0.f,0.f);//x轴

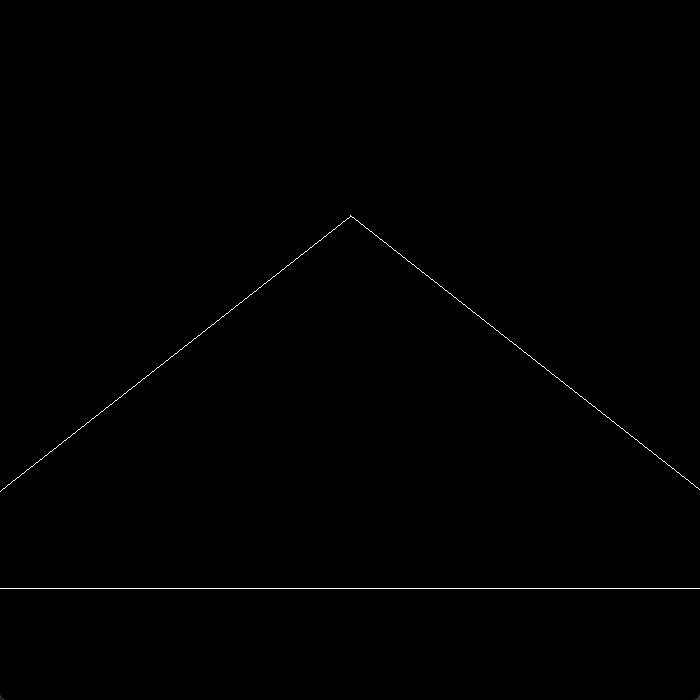
接着是修改while循环中的r.set_model函数，为什么修改这个呢，因为set_model就是设置模型的位置矩阵（旋转平移），那么只要将我们的旋转矩阵相乘这个矩阵就相当于设置了模型的矩阵。修改后的函数为：r.set_model(get_rotation(RotationAxis, angle2)*get_model_matrix(angle));
下面是旋转的情况(绕x轴，因为三角形的z坐标是-2，所以转的时候不是沿着三角形的最下面一条边转的)：

GAMES101-Lecture 05 Rasterization 1 (Triangles) & 作业1

Transformation

Perspective Projection

Canonical Cube to Screen

Frame Buffer: Memory for a Raster Display

LCD(Liquid Crystal Display) Pixel(液晶显示)

LED Array Display 发光二极管

Triangles-Fundamental Shape Primitives

Sampling

作业1

作业1重做版

相关文章

GAMES101-Lecture 01 Overview of Computer Graphics

GAMES101-Lecture 02 Review of Linear Algebra

GAMES101-Lecture 03 Transformation