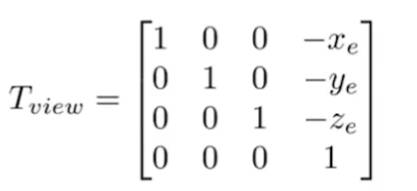GAMES101-Lecture 04 Transformation Cont. & 作业0

这一节其实是一部分变换的内容和观测(Viewing)的内容，按理说变换应该放到上一章，所有的观测放在一章

3D Transforms

• 再一次使用齐次坐标

• 3D point =$ (x,y,z,1)^T$

• 3D vector =$ (x,y,z,0)^T$

• 使用4×4的矩阵表示仿射变换

\[\left( \begin{matrix} x\prime\\ y\prime\\ z\prime\\ 1 \end{matrix} \right)= \left( \begin{matrix} a & b & c & t_x\\ d & e & f & t_y\\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{matrix} \right)\cdot \left( \begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right)\]

• 是先做的旋转再做的平移

3D Transformations

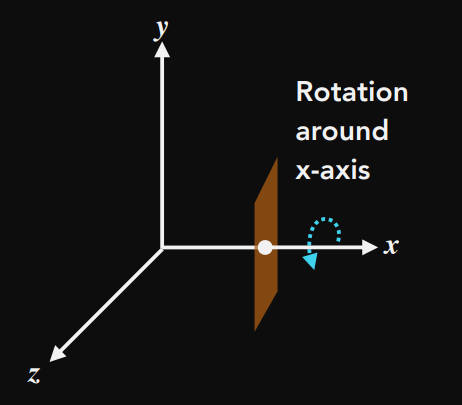
• Rotation:

• 绕x轴旋转，x坐标是不变的

  \[R_x(\alpha) = \left( \begin{matrix} 1 & 0 & 0 & 0\\ 0 & \cos\alpha & -\sin\alpha & 0\\ 0 & \sin\alpha & \cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right)\]

• 绕y轴旋转，y轴有所不同，是因为$z\times x$得到Y轴，而不是$x\times z$得到Y轴，如果是$x\times z$得到Y轴，那么矩阵内元素应该和其他一样，不会反。

  \[R_x(\alpha) = \left( \begin{matrix} \cos\alpha & 0 & \sin\alpha & 0\\ 0 & 1 & 0 & 0\\ -\sin\alpha & 0 & \cos\alpha & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right)\]

• 绕z轴旋转

  \[R_x(\alpha) = \left( \begin{matrix} \cos\alpha & -\sin\alpha & 0 & 0\\ \sin\alpha & \cos\alpha & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right)\]

3D Rotation

• 将旋转分解为三个轴方向的旋转，这三个角称为欧拉角

  \[R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_z(\gamma)\]

• Rodrigues’ Rotation Formula(这个公式并没有讲推导，应该是直接用):默认n向量是过原点的，沿着n向量旋转α角度，后面那个矩阵是指：通过矩阵的方式计算叉乘。想绕任意n向量，就需要借助平移来实现。

  \[R(\pmb{n},\alpha) = cos(\alpha)\pmb{I}+ (1-\cos(\alpha))\pmb{nn^T}+\sin(\alpha) \left( \begin{matrix} 0 & -n_z & n_y\\ n_z & 0 & -n_x\\ -n_y & n_x & 0 \end{matrix} \right)\]

• 由于矩阵难以插值，提出了四元数来解决（具体没讲）

Viewing transformation(观测变换)

• 模型变换->视图变换->投影变换（简称MVP变换）
• 先摆好模型的位置方向，再摆好摄像机的位置和方向，最后把摄像机和模型同时移动，将相机放在原点，注视方向是-z，向上方向为y，进行投影变换（后续还有一个视口变换）

View/ Camera Transformation

• 定义相机：

  • 位置:$\vec{e}$

  • 注视方向:$\hat{g}$

  • 向上方向:$\hat{t}$

• 重要的观测：

  • 将相机放在原点，注视方向是-z，向上方向为y

• 先平移，再旋转$M_{view}=R_{view}T_{view}$

• 平移矩阵比较简单就不写了，旋转矩阵不直接旋转相机，而是先求世界坐标系旋转到相机的旋转矩阵，然后再求一个逆。也就是将X轴旋转到（g×t），Y轴旋转到t，Z轴旋转到-g。

• 下面矩阵里的元素是相机坐标系的基向量

  \[R_{view}^{-1}= \left[ \begin{matrix} x_{\hat{g}\times\hat{t}} & x_t & x_{-g} & 0\\ y_{\hat{g}\times\hat{t}} & y_t & y_{-g} & 0\\ z_{\hat{g}\times\hat{t}} & z_t & z_{-g} & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right] \Rightarrow R_{view}= \left[ \begin{matrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0\\ x_t & y_t & z_t & 0\\ x_{-g} & y_{-g} & z_{-g} & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]\]

• 那么怎么理解呢，可以假设旋转矩阵乘以一个列向量$(1,0,0)^T$，也就是x轴的单位向量，结果是$(x{\hat{g}\times\hat{t}},y_{\hat{g}\times\hat{t}},z_{\hat{g}\times\hat{t}})^T$

Projection transformation

• 正交投影和透视投影

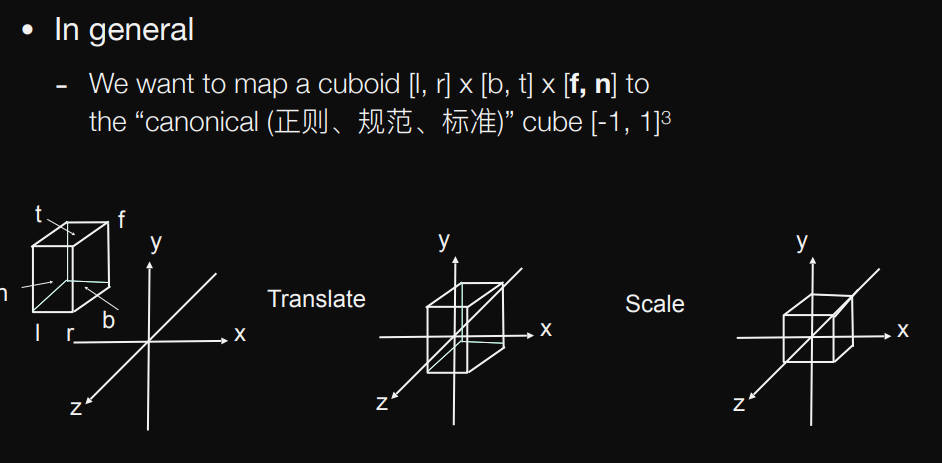
Orthographic Projection

• 因为是看向-z方向，所以f小于n

• 将长方体$[l,r]\times[b,t]\times[\pmb{f,n}]$平移到原点，再缩放成canonical标准正方体$[-1,1]^3$缩放长宽高至2（因为是-1到1），下面是平移和缩放的矩阵：

  \[M_{ortho}= \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 & -\frac{r+l}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & -\frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{matrix} \right]\]

• 这次变换确实会引起原来物体的拉伸但最后还有一个视口变换会再次拉伸

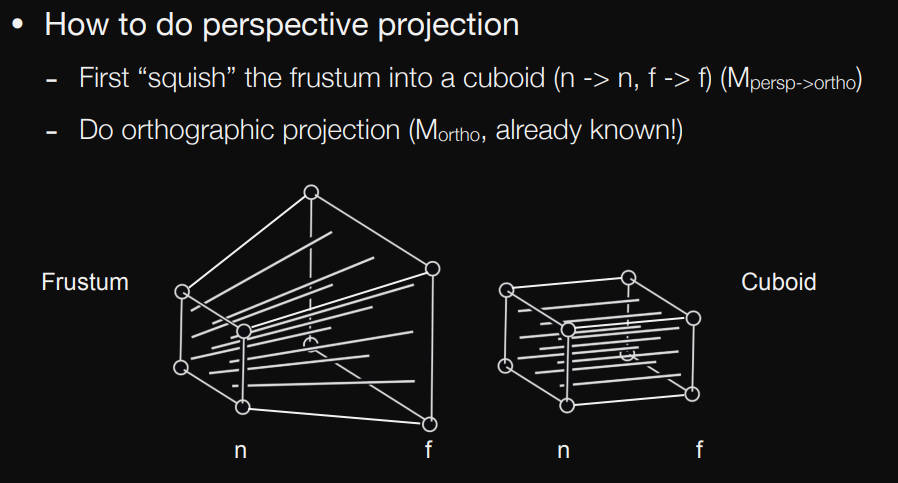
Perspective Projection

• 先把平截头体（frustum）挤成长方体，然后再做一次正交投影

• 规定：1. 近平面永远不变2. 近平面和远平面z不会变化3. 远平面的中心点不变

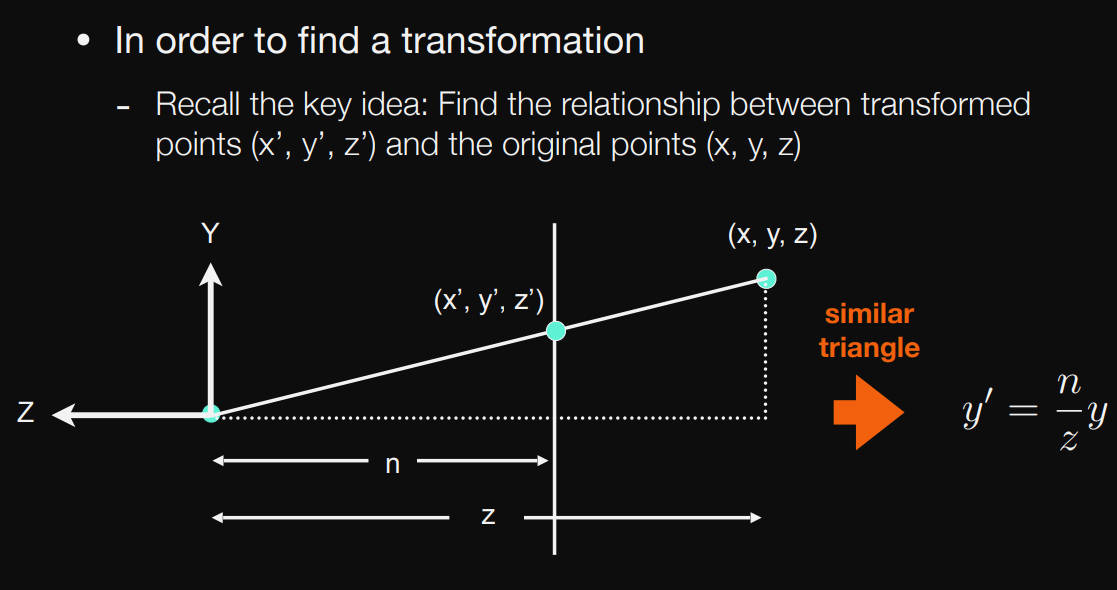
• $y\prime=\frac{n}{z}y$ ，$x\prime=\frac{n}{z}x$（$x\prime,y\prime指远平面变换后的坐标$）

• 其实z是一个变量，不同的z代表不同远近的点，z也可以等于n，这样的话变换后的坐标还是原来的那个坐标

• 那么现在就是说需要一个矩阵乘以坐标后能够成为：

  \[M_{persp\rightarrow ortho}^{(4\times 4)} \left( \begin{matrix} x\\ y\\ z\\ 1 \end{matrix} \right) \Rightarrow \left( \begin{matrix} \frac{nx}{z}\\ \frac{ny}{z}\\ unknown\\ 1 \end{matrix} \right) == \left( \begin{matrix} nx\\ ny\\ still unknown\\ z \end{matrix} \right)\]

• 然后可以推导出部分矩阵

  \[M_{persp\rightarrow ortho}^{(4\times 4)} = \left[ \begin{matrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & 1 & 0 \end{matrix} \right]\]

• 观察：

  • 近平面任何点都不变，也就是说$(x,y,n)$经过$M_{persp\rightarrow ortho}^{(4\times 4)}$变换后，还是$(x,y,n)$这个点

• 远平面z都不变，也就是说远平面中心点$(0,0,f)$经过$M_{persp\rightarrow ortho}^{(4\times 4)}$变换后也不变

• 把近平面的点代到公式中，即让z=n，那么

  \[\left( \begin{matrix} x\\ y\\ n\\ 1 \end{matrix} \right) == \left( \begin{matrix} nx\\ ny\\ n^2\\ n \end{matrix} \right)\]

• 所以$M_{persp\rightarrow ortho}^{(4\times 4)}$的第三行(0 0 A B)

\[\left( \begin{matrix} 0 & 0 & A & B \end{matrix} \right)\left( \begin{matrix} x\\ y\\ n\\ 1 \end{matrix} \right) = n^2\]

• 取远平面的中心点(0,0,f)，代到公式中

  \[\left( \begin{matrix} 0\\ 0\\ f\\ 1 \end{matrix} \right) == \left( \begin{matrix} 0\\ 0\\ f^2\\ f \end{matrix} \right)\]

• 那么得到两个式子：

  \[An + B = n^2\\ Af + B = f^2\]

• 解出

  \[A=n+f\\ B=-nf\]

• 最后，终于解出了矩阵$M_{persp\rightarrow ortho}^{(4\times 4)}$

• \[M_{persp\rightarrow ortho}^{(4\times 4)} = \left[ \begin{matrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0 \end{matrix} \right]\]

• 那么，透视投影矩阵：

  \[M_{persp}=M_{ortho}M_{persp\rightarrow ortho}\]

作业0

• 作业描述：给定一个点 P=(2,1), 将该点绕原点先逆时针旋转 45◦，再平移 (1,2), 计算出

  变换后点的坐标（要求用齐次坐标进行计算）。

• 先配置环境，我没有按照文档里的使用虚拟机，直接给我vs2022安装Eigen库了，很简单，参考博客：Eigen库下载安装并配置到VS_勤勉的一只洋的博客-CSDN博客_eigen库下载

• 配置完后，可以先读读Eigen的官方文档:Eigen: Matrix and vector arithmetic

• 然后可以把框架里没有的代码试着补全（和、乘、点积、叉积等）：

  #include<cmath>
  #include<Eigen/Core>
  #include<Eigen/Dense>
  #include<iostream>
    
  int main()
  {
      // Basic Example of cpp
      std::cout << "Example of cpp \n";
      float a = 1.0, b = 2.0;
      std::cout << a << std::endl;
      std::cout << a / b << std::endl;
      std::cout << std::sqrt(b) << std::endl;
      std::cout << std::acos(-1) << std::endl;
      std::cout << std::sin(30.0 / 180.0 * acos(-1)) << std::endl;
    
      // Example of vector
      std::cout << "Example of vector \n";
      // vector definition
      Eigen::Vector3f v(1.0f, 2.0f, 3.0f);
      Eigen::Vector3f w(1.0f, 0.0f, 0.0f);
      // vector output
      std::cout << "Example of output \n";
      std::cout << v << std::endl;
      // vector add
      std::cout << "Example of add \n";
      std::cout << v + w << std::endl;
      // vector scalar multiply
      std::cout << "Example of scalar multiply \n";
      std::cout << v * 3.0f << std::endl;
      std::cout << 2.0f * v << std::endl;
    
      // Example of matrix
      std::cout << "Example of matrix \n";
      // matrix definition
      Eigen::Matrix3f i, j;
      i << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
      j << 2.0, 3.0, 1.0, 4.0, 6.0, 5.0, 9.0, 7.0, 8.0;
      // matrix output
      std::cout << "Example of output \n";
      std::cout << i << std::endl;
      // matrix add i + j
      std::cout << i + j << std::endl;
      // matrix scalar multiply i * 2.0
      std::cout << i * 2.0 << std::endl;
      // matrix multiply i * j
      std::cout << i * j << std::endl;
      // matrix multiply vector i * v
      std::cout << i * v << std::endl;
      //dot product
      std::cout << v.dot(w) << std::endl;
      //cross product
      std::cout << v.cross(w) << std::endl;
    }
  

• 在最后实现了题目：

      //P点
      Eigen::Vector3f P(2.0, 1.0, 1.0);
      //变换矩阵
      Eigen::Matrix3f transform;
      //可以直接写一个矩阵，因为先旋转再平移
      transform << std::cos(45.0 / 180.0 * acos(-1)), -std::sin(45.0 / 180.0 * acos(-1)), 1.0,
          std::sin(45.0 / 180.0 * acos(-1)), std::cos(45.0 / 180.0 * acos(-1)), 2.0,
          0.0, 0.0, 1.0;
      //变换后的点：
      Eigen::Vector3f Pprime;
      Pprime = transform * P;
      std::cout << Pprime;
  

• 答案：

  \[P\prime = \left( \begin{matrix} 1.70711\\ 4.12132\\ 1 \end{matrix} \right)\]