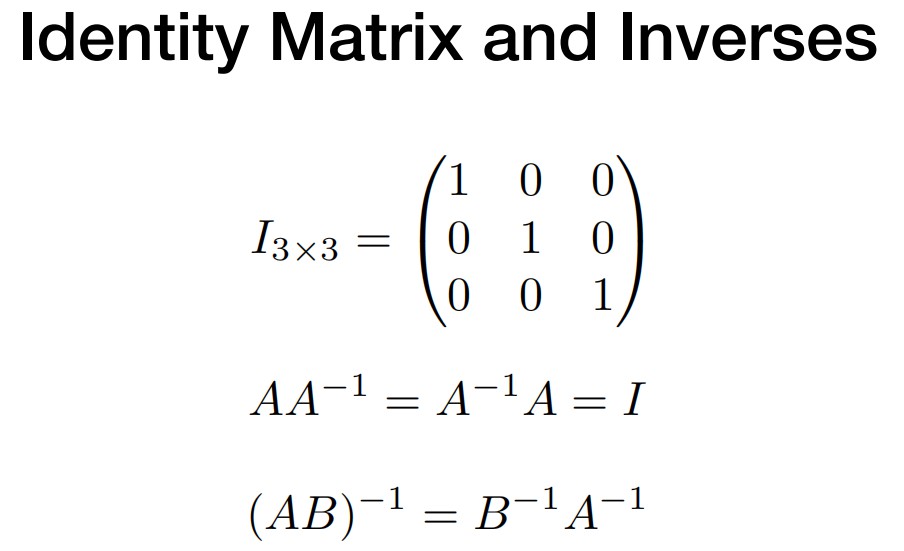GAMES101-Lecture 02 Review of Linear Algebra

阅读材料：第 2 章（Miscellaneous Math）；第 5 章（Linear Algebra）

1. Graphics’ Dependencies

• 基础数学：线代、微积分、统计

• 基础物理：光学、力学

• 其它：信号处理、数值分析

2. This Course

• More dependent on linear algebra

  • 向量、矩阵

3. Vector

• 写作$\vec{a}$或者a

• 表示方向和长度

• 没有绝对的开始位置

4. Vector Normalization

• 向量的模（长度）$\lVert{\vec{a}}\rVert$

• 单位向量：$\hat{a}=\frac{\vec{a}}{\lVert{\vec{a}}\rVert}$

5. Vector Addion

• 平行四边形法则、三角形法则

6. Cartesian Coordinates

• 向量默认是列向量 $A=\left(\begin{matrix}x\y\end{matrix}\right)$

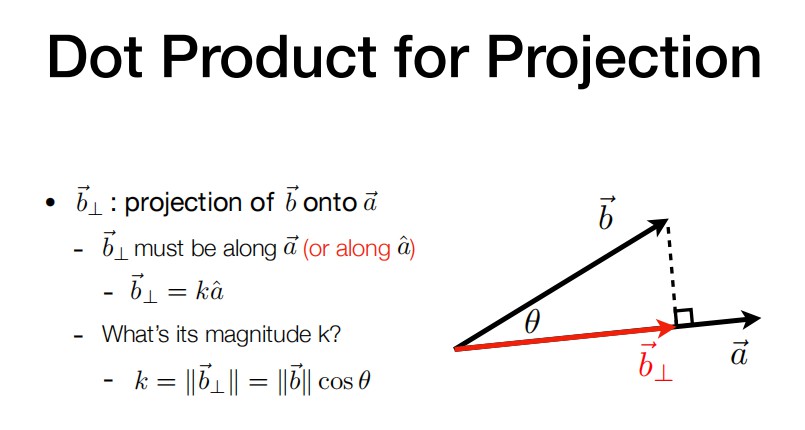
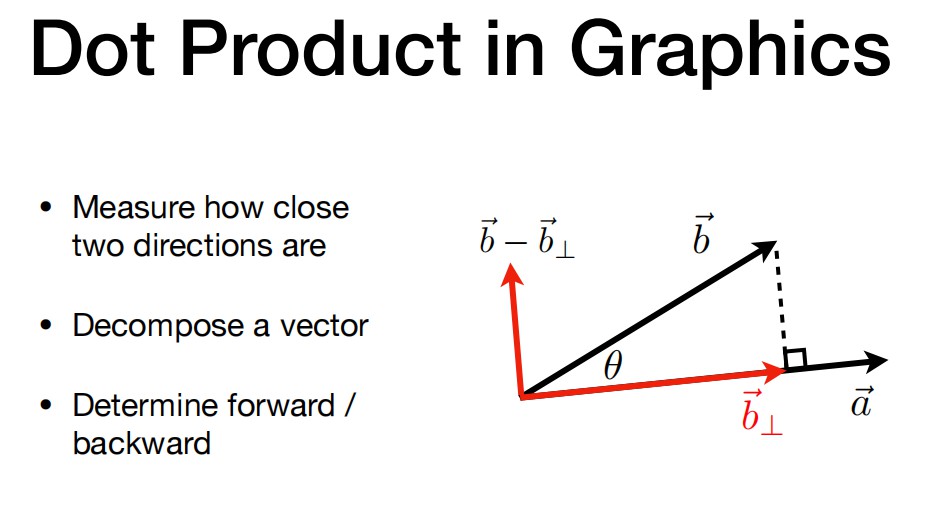
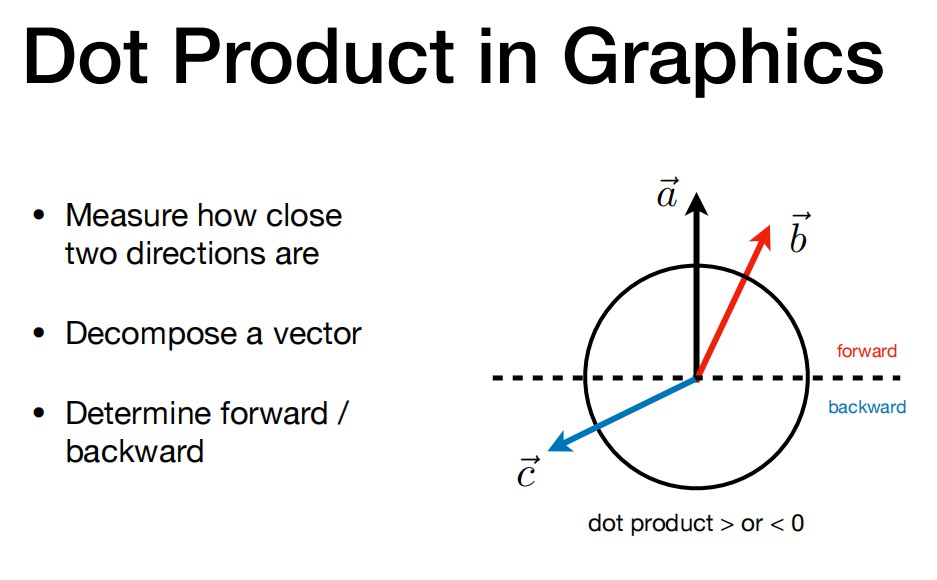
7. Vector Multiplication

• 点乘

  • 计算两个向量间距远近

  • 分解向量

  • 决定向量的前后

• 投影

  

• 投影可以用来计算一个向量平行与另一个向量和垂直于另一个向量的分向量

• 通过点成结果的正负来判断向量的前后，判断两个向量是不是相反的

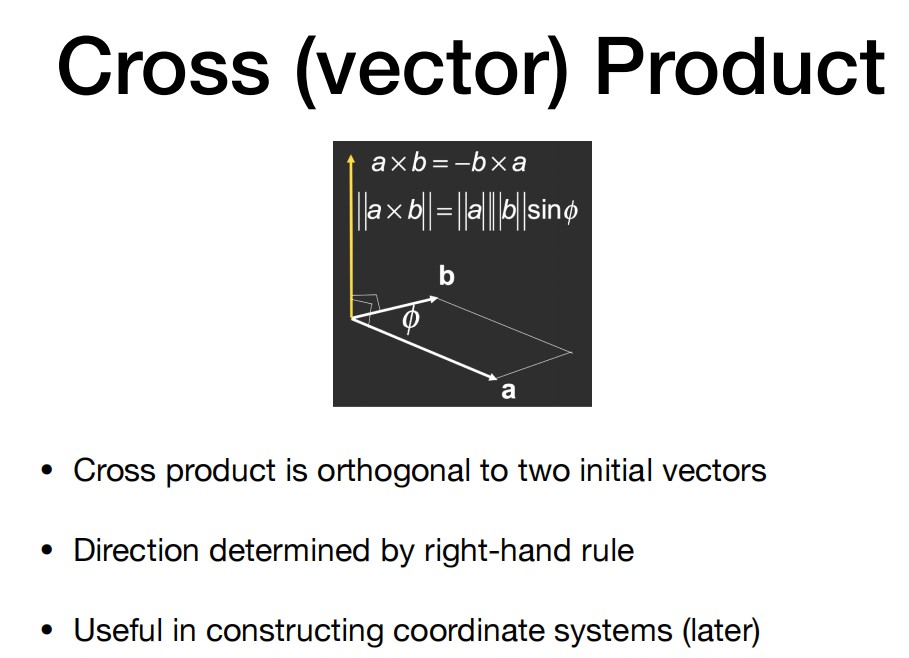
• 叉乘

• $\vec{a}\times \vec{a}=\vec{0}$

• 右手坐标系：$\vec{x}\times\vec{y}=+\vec{z}$

• 左手坐标系：$\vec{x}\times\vec{y}=-\vec{z}$(一些图形API用的左手系)

• 叉乘运算：

• 判定左右：假设向量a和b在xy平面上，向量a叉乘b，结果向量是正的（也就是说与Z轴同向），说明b在a的左侧

• 判定内外：有一个三角形ABC，和一个点P，判断P是否在ABC内，如果$\vec{AB}\times\vec{AP}$和$\vec{BC}\times\vec{BP}$和$\vec{CA}\times\vec{CP}$的结果都是+或者-，那么就在三角形内。也可以说P点在三条边的左边或者右边

• 正交基和坐标系

8. Matrices

• 矩阵-矩阵相乘

  • 两个矩阵A、B相乘得到C，如果要算C的某个元素，比如第二行第三列，那么就找A的第二行和B的第三列，做一个点积，就是该元素的结果

  • 没有交换律但有结合律

• 矩阵-向量相乘

• 矩阵转置

  • $(AB)^T=B^TA^T$

• 单位矩阵

• 定义了矩阵的逆

• 对角矩阵、逆矩阵

• 以矩阵形式的向量乘积

  • 点积：$\vec{a}\cdot\vec{b}=\vec{a}^T\vec{b}$

  • 叉积：$\vec{a}\times\vec{b}=A^*b$(A是一个矩阵)