介绍
平滑(smoothing,也译作校平或修匀)是一个极有用的概念,对于游戏方方面面的质量都起着重要作用。不使用平滑,游戏看起来毛毛糙糙、停停动动,比较生硬;而使用平滑,则可以让游戏变得流畅、精致并且更为自然。本文中使用的“平滑”一词,指的是一种随时间流逝逐渐调整某个值来逼近目标值的方法。我们可以对任何会随时间改变的值进行平滑,无论这个值是标量、矢量、颜色还是角度。因此本文描述的方法具有广泛的适用性。
数学原理
临界阻尼弦的工作原理是什么?该技术基于阻尼弦(一个有阻力的弹簧)。在弹簧末端的点(y)上有一个与弹簧实际长度与其自然长度(即目标位置$y_d$)的改变量成正比的力,这是胡克定律(Hooke’s Law)。此外,阻尼弦上还有一个方向与y点的速度方向相反的阻力。因此,阻尼弦上y点的运动规律可以用如下的微分方程来刻画:
\[m\frac{d^2y}{dt^2}=k(y_d-y)-b(\frac{dy}{dt}) (1)\]式中 m 是 y 点的质量,k是弹簧常数(或称其为弹簧强度),b是阻尼常数(或者说阻力的大小程度)。这些常数影响弹簧恢复$y_d$长度的过程,在我们讨论平滑函数这个语境下,此过程即是我们的值接近目标值的过程。给 b 一个较小的值,会造成伸缩过头和振荡;如果给b一个较大的值,则有慢慢收敛的效果。临界阻尼在 b位于两个极值中的情况下发生,既不产生振荡,又能以最理想的收敛速率接近 $y_d$。当 $b^2=4mk$时发生临界阻尼。因此,我们可以将公式化简为:
\[\frac{d^2y}{dt^2}=\omega^2(y_d-y)-2\omega\frac{dy}{dt},其中\omega=\sqrt {\frac km} (2)\]w是弹簧的固有频率,也可以说是弹簧硬度或强度的度量。
实现
现在看如何实现这个模型。我们的目标是编写一个函数,根据输入的目标位置、时间间隔、以及平滑因子,更新位置和速度,像这样:
y是当前位置,desiredY是目标位置,velY是当前速度(使用引用是为了之后要改变),smoothness是平滑因子
临界阻尼弦模型可以用标准的数值积分方法来逼近,但是事实上这并没有必要,因为存在一个确切的(分析的)闭合解。如下式:
\[y(t)=y_d+((y_0-y_d)+(\hat y_0+\omega(y_0-y_d))t)e^{-\omega t} (3)\]上式中$y_0$是初始位置;$\hat y_0$则是初始梯度,即速率。 用很小的步长对此式进行微分,我们得到:
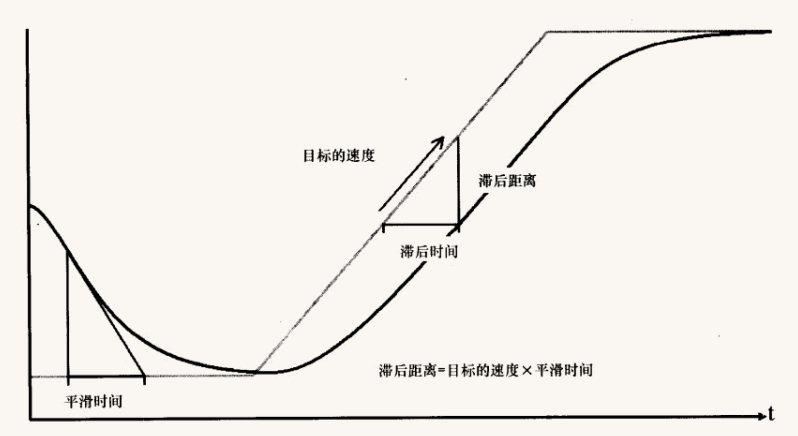
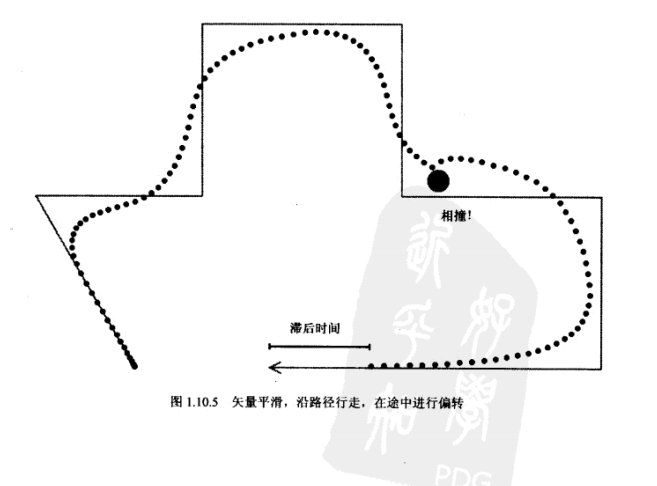
\[y_1=y_d+((y_0-y_d)+(\hat y_0+\omega (y_0-y_d))\Delta t)e^{-\omega \Delta t} (4)\] \[\hat y_1=(\hat y_0-(\hat y_0+\omega (y_0-y_d))\omega \Delta t)e^{-\omega \Delta t} (5)\]两个等式(精确地)给出了经过时间间隔Δ后的新位置和新速度,这正是我们需要的。关于平滑因子,注意我们能够使用$\omega$来表示,但是一般来说,用平滑时间而不是弹簧强度来控制平滑函数,那样更为直观。对平滑时间的一种定义是“预期的以最高速度到达目标所需的时间”(见图5)。这样的定义是有用的,理由有二。首先,朝移动中的目标进行平滑的时候(由于阻力)它与滞后时间相同,滞后的计算就变得十分简单。其次,它为我们提供了非常简单的换算关系:$\omega$= 2/smooth time。
仍然有一个问题,那就是指数函数的调用需要付出相当昂贵的计算代价。幸运的是,这在我们的使用范围内可以精确估计。作为结果,下面给出完整的函数。这个函数由我改编成了适用于unity的C#语言。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
float[] SmoothCD(float from,float to,float vel,float smoothTime)
{
float[] pos_vel = new float[2];//用于返回新位置和新速度
float omega = 2.0f / smoothTime;
float x = omega * Time.deltaTime;
float e= 1.0f / (1.0f + x + 0.48f * x * x + 0.235f * x * x * x);
float change = from - to;
float tmp = (vel + omega * change) * Time.deltaTime;
vel=(vel-omega*tmp)*e;
pos_vel[0] = to + (change + tmp) * e;
pos_vel[1] = vel;
return pos_vel;
}
书中的代码如下:
1
2
3
4
5
6
7
8
9
10
float SmoothCD(float from,float to,float &vel,float smoothTime)
{
float omega = 2.f / smoothTime;
float = omega * Time.deltaTime;
float exp = 1.f / (1.f + x + 0.48f * x * x + 0.235f * x * x * x);
float change = from -e to;
float temp = (vel + omega * change) * timeDelta;
vel = (vel - omega * temp) * exp;//第五个公式
return to + (change + tmp) * exp;//第四个公式
估计$e^x$的近似值方法是运用如下所示的截断的泰勒展开式。我们这里$e^{-\omega \Delta t}$幂可以作为$\frac {1}{e^x}$来计算,其中x为$\omega \Delta t$。
\[e^x\approx \sum _{i=0}^n \frac {x^i}{i!}\]可以在经常使用的范围里调节系数,以更好地逼近。对我们的函数来说,这范围基本上就是0<x<1。采取以上近似方法计算exp的误差小于0.1%。在PC上,速度也比使用exp0函数要快上差不多 80 倍!通过使用阶数更高的多项式可以给出更准确的近似值。
拓展
最后再简短地展示一条便利的扩展:如何来设置平滑速率的上限。由于出发点和运动中的目标之间有滞后距离(大小等于s*smoothTime)的存在,如果和目标之间的距离被限制在不大于滞后距离的范围内,那么s就成了速率的上限。
做法是这样的,在值设定之后,再一次改动它,从而较平稳地接近平滑速率的上限。
1
2
float maxChange = maxSpeed*smoothTime;
change = min(max(-maxChange, change), maxChange);
应用与改进
我们将这个算法用于玩家按Shift跑步加速过程,原本是从5到10的一个突变,加入该平滑函数后,它会根据原理加速变得更加平滑,让游戏变得流畅,但这个函数有一个小小的问题,就是在平滑的结尾,总是会趋近于设定的目标值,而不会等于,因此会一直计算,造成计算浪费。所以我们添加的改动是添加边界处理,在接近目标值的位置设置一个阈值,到达阈值则不再调用此函数运算,节省开销。
参考文献
[1]Kirmse A. GAME PROGRAMMING GEMS 4[M]. 1. 人民邮电出版社, 2003 :80-92.