力扣-使用最小花费爬楼梯 & 不同路径 & Vector二维数组初始化方法

746. 使用最小花费爬楼梯

class Solution {
public:
//动规五部曲
//1.确定dp数组以及下标的含义
//爬到第i阶的台阶需要的花费为dp[i]
//2.确定递推公式
//dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
//3.初始化dp数组
//4.遍历顺序，从前往后
//5.实例2推导
//  dp数组：0  0  1 2 2 3   3 4 4   5  6
//cost数组：1 100 1 1 1 100 1 1 100 1
    int minCostClimbingStairs(vector<int>& cost) {
        int dp[2];
        //初始化dp数组
        dp[0] = 0;
        dp[1] = 0;
        //遍历
        for(int i = 2; i <= cost.size(); i++)
        {
            int tmp = min(dp[1] + cost[i - 1], dp[0] + cost[i - 2]);
            dp[0] = dp[1];
            dp[1] = tmp;
        }
        return dp[1];
    }
};

    本质上和昨天的爬楼梯是一样的，动规五部曲就可以轻松解决，不一样的就在于递推公式不太一样。

62. 不同路径

class Solution {
public:
//动规五部曲
//1.确定dp数组和下标的含义
//到达坐标为（i，j）的格子的路径数目为dp[i][j]
//2.确认递推公式
//dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
//3.dp数组初始化
//其实只需要初始化上边和左边一条线，但为了方便就全初始化1了，因为不影响
//4.遍历顺序，从（1，1）开始从左往右，一行一行地遍历
//5.示例1推导（从1，1）开始
// 2 3 4  5  6  7
// 3 6 10 15 21 28

    int uniquePaths(int m, int n) {
        //创建数组并初始化：
        vector< vector<int> > dp(m, vector<int>(n, 1));
        //遍历
        for(int i = 1; i < m; i++)
        {
            for(int j = 1; j < n; j++)
            {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};

    这道题和上一道题也很类似，使用动规五部曲就可以轻松化解，不同的是这个题目需要用到二维数组，正好记录一下c++ vector二维数组的三种初始化方法：

C++ Vector二维数组初始化方法

第一种

int m = 10;
int n = 10;
//只是开辟空间
vector< vector<int> > dp(m, vecor<int> (n));
//所有元素初始化为1
vector< vector<int> > dp(m, vecor<int> (n, 1));

第二种

int m = 10;
int n = 10;

vector< vector<int> > dp = vector< vector<int> >(m, vecor<int> (n));

第三种

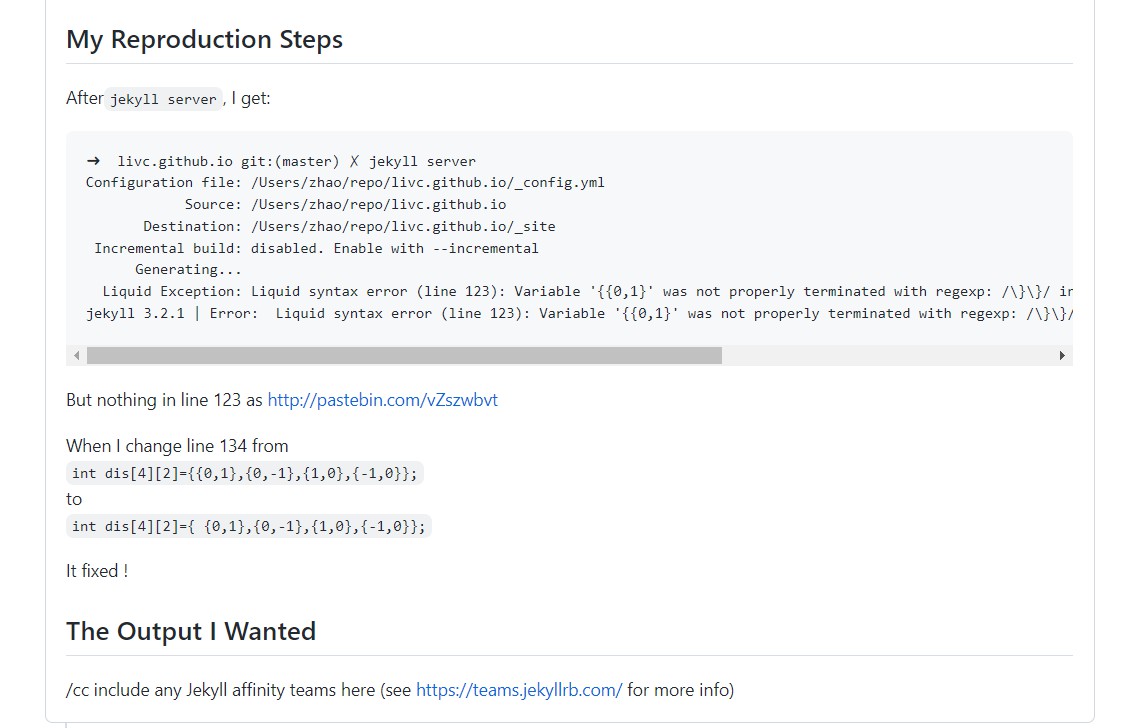
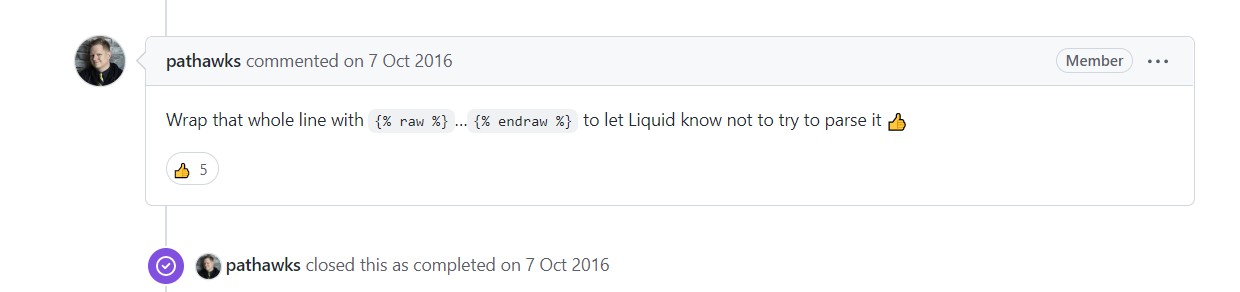
不知道为啥{ {1,2,3},{4,5,6}};总是报错，上传不上去了……

int m = 2;
int n = 3;

 vector< vector >dp(m, vecor (n)) = {{1,2,3},{4,5,6}};

    Google了一下，发现改法挺搞笑的哈哈哈哈：

    然后发现加个空格还是不行……试试这个

    蚌埠住了 ……上面两种方法都可以，一直报错是因为“不知道为啥{ {1,2,3},{4,5,6}};总是报错，上传不上去了……”这句话一开始我没加空格也没加raw标签。